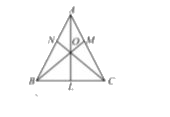
A point O is taken inside an equilateral $△$ ABC. If OL $⊥$ BC, OM $⊥$ AC and ON $⊥$ AB such that OL = 14 cm, OM = 10 cm and ON = 6 cm, then find the area of $△$ ABC

A

$300 \sqrt{3} c m^{2}$

B

$200 \sqrt{3} c m^{2}$

C

$300 c m^{2}$

D

$325 \sqrt{2} c m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

|

Answer

Step by step video, text & image solution for A point O is taken inside an equilateral triangle ABC. If OL bot BC, OM bot AC and ON bot AB such that OL = 14 cm, OM = 10 cm and ON = 6 cm, then find the area of triangleABC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a triangle ABC, AB = 8 cm, AC = 10 cm and $∠ B = 90^{\circ}$ , then the area of $Δ A B C$ is
A49 sq. cm
B36 sq. cm
C25 sq. cm
D24 sq. cm
Question 2 - Select One
In the given figure, $A B ⊥ A D, B C ⊥ B D$ and AD = 9 cm, BC = 8 cm and CD= 17 cm. Find the area of quadrilateral ABCD

A112 $c m^{2}$
B114 $c m^{2}$
C119 $c m^{2}$
D117 $c m^{2}$
Question 3 - Select One
In a $△ A B C$ ,AB = AC and $A D ⊥ B C$ , then :
A $A B < A D$
B $A B > A D$
CAB=AD
D $A B \leq A D$

SCIENCE OLYMPIAD FOUNDATION -IMO QUESTION PAPER 2016 SET A-MATHEMATICAL REASONING

Home
Ask Doubt
Profile