प्रश्न 23 और 24 के लिए अनुच्छेद
माना कि f(x)=(1−x)2sin2x+x2 जहाँ x∈R और g(x)=∫x1(2(t−1)t+1−lnt)f(t)dt, जहाँ x∈(1,∞)
दिये गये कथन हैं:
P: एक ऐसी संख्या x∈R का अस्तित्व है जिसके लिए f(x)+2x=2(1+x2)
Q: एक ऐसी संख्या x∈R का अस्तित्व है जिसके लिए 2f(x)+1=2x(1+x)
तब निम्न में से कौनसा कथन सही?
P और Q दोनों सत्य हैं.
P सत्य है और Q असत्य है
P और Q दोनों असत्य हैं
P असत्य है और Q सत्य है
Step by step video & image solution for प्रश्न 23 और 24 के लिए अनुच्छेद माना कि f(x) = (1-x)^(2) sin^(2) x + x^(2) जहाँ x in R और g(x) = int_(1)^(x) ((2( t-1) )/( t+1) - lnt ) f(t) dt, जहाँ x in (1,oo) दिये गये कथन हैं: P: एक ऐसी संख्या x in RR का अस्तित्व है जिसके लिए f(x) + 2x = 2 (1 + x^(2) ) Q: एक ऐसी संख्या x in RR का अस्तित्व है जिसके लिए 2f(x) + 1= 2x ( 1+ x) तब निम्न में से कौनसा कथन सही? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2012)EXERCISE - भाग - III : गणित खंड - III : बहुल सही उत्तर प्रकार6videos
JEE ADVANCED पेपर - 2 (2012)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2012)EXERCISE - भाग - III : गणित खंड - III : बहुल सही उत्तर प्रकार6videos
JEE ADVANCED पेपर - 2 (2012)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 1 (2021)EXERCISE - MATHEMATICS (खंड- 3)9videos
JEE ADVANCED पेपर - 1 (2021)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2013)EXERCISE - PART III : MATHEMATICS (खण्ड - 3) (सुमेलन सूची प्रकार)4videos
JEE ADVANCED पेपर - 2 (2013)
Similar Questions
दो घटनायें X और Y इस प्रकार की हैं कि P(X∣Y)=12,P(Y∣X)=13 और P(XnY)=16 तब निम्न में से कौन कथन सही है/हैं?
05:49View Solutionदो घटनायें X और Y इस प्रकार की हैं कि P(X∣Y)=12,P(Y∣X)=13 और P(XnY)=16 तब निम्न में से कौन कथन सही है/हैं?
03:29View Solutionकिसी 3×3 आव्यूह M के लिए, माना |M| ,M के सारणिक को निरूपित करता है। माना
E=⎡⎢⎣12323481318⎤⎥⎦,P=⎡⎢⎣100001010⎤⎥⎦ तथा F=⎡⎢⎣13281813243⎤⎥⎦
यदि Q कोटि 3×3 का एक व्युत्क्रमणीय आव्यूह है, तब निम्न में से कौनसा/कौनसे कथन सही है/हैं?08:58View Solutionसूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिए गए कोड का प्रयोग करके सही उत्तर चुनिये :
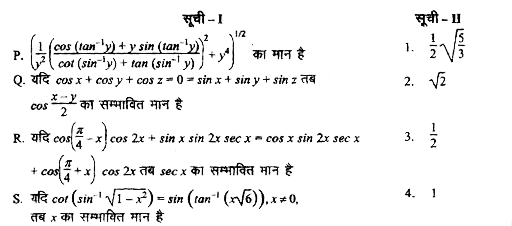 09:05View Solution
09:05View SolutionLet F(x)=f(x)+f(1x),w h e r ef(x)=∫xtlogt1+tdt. (1) 12 (2) 0 (3) 1 (4) 2
01:24View SolutionIf f(x)=1+x+int_(1)^(x)(ln^(2)t+2ln t)dt then f(x) increases in
02:21View SolutionLet f(x)=(1−x)2sin2x+x2 for all x∈IR, and let g(x)=∫x1(2(t−1)t−1−lnt)f(t) dt for all x,∈(1,∞). Consider the statements: P: There exists some x∈IR such that f(x)+2x=2(1+x2) Q: There exists some x∈IR such that 2f(x)+1=2x(1+x) Then
03:19View SolutionLet f(x)=(1−x)2sin2x+x2 for all x∈IR, and let g(x)=∫x1(2(t−1)t−1−lnt)f(t) dt for all x,∈(1,∞). Which of the following is true?
View SolutionIf int_(0)^(x)f(t)dt=x^(2)+int_(x)^(1)t^(2)f(t)dt, then f'((1)/(2)) is
06:01View SolutionIf f(x)=∫x0{f(t)}−1dt, and ∫10{f(t}−1dt=√2, then f(x)=
05:23View SolutionLet f(x)=∫x3x2dtlnt for x>1andg(x)=∫x1(2t2−lnt)f(t)dt(x>1), then:
02:05View SolutionLet f(x)=1(1−x)2sin2x+x2 for all x∈IR, and let g(x)=x∫1(2(t−1)t+1−lnt)f(t)dt for all x∈(1,∞)
Which of the folloiwng is true ?07:13View SolutionLet f(x)=(1−x)2sin2x+x2 for all x∈R, and let g(x)=∫x1(2(t−1)t+1−logt)f(t)dt for all x∈(1,∞).
Consider the statements :
P : there exists some x∈R such that
f(x)+2x=2(1+x2)
Q : There exists some x∈R such that
2f(x)+1=2x(1+x) then-06:22View SolutionLet f(x)=(1−x)2sin2x+x2 for all x∈R, and let g(x)=∫x1(2(t−1)t+1−logt)f(t)dt for all x∈(1,∞).
Which of the following is true?05:30View SolutionIf ∫1sinxt2f(t)dt=1−sinx, then the value of f(1√3) is :
01:57View SolutionIf int_(0)^(x) f(t)dt = x^(2) + int_(x)^(1)t^(2)f(t)dt If so f'(1//2) is
06:14View Solution

