त्रिभुज POR, में P बृहत्तम कोण है तथा cosP=13 इसके अतिरिक्त त्रिभुज का अंत:वृत्त भुजाओं PO, OR तथा RP को क्रमश: N, L तथा M पर इस तरह स्पर्श करता है कि PN, OL तथा RM की लम्बाइयाँ क्रमागत सम पूर्णसंख्याएँ हैं । तब त्रिभुज की भुजा (भुजाओं) की सम्भावित लम्बाई (लम्बाइयाँ) है (हैं)
16
18
24
22
Step by step video & image solution for त्रिभुज POR, में P बृहत्तम कोण है तथा cos P= 1/3 इसके अतिरिक्त त्रिभुज का अंत:वृत्त भुजाओं PO, OR तथा RP को क्रमश: N, L तथा M पर इस तरह स्पर्श करता है कि PN, OL तथा RM की लम्बाइयाँ क्रमागत सम पूर्णसंख्याएँ हैं । तब त्रिभुज की भुजा (भुजाओं) की सम्भावित लम्बाई (लम्बाइयाँ) है (हैं) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2013)EXERCISE - PART III : MATHEMATICS (खण्ड -2) (अनुच्छेद प्रकार)8videos
JEE ADVANCED पेपर - 2 (2013)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2013)EXERCISE - PART III : MATHEMATICS (खण्ड - 3) (सुमेलन सूची प्रकार)4videos
JEE ADVANCED पेपर - 2 (2013)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2012)EXERCISE - भाग - III : गणित खंड - III : बहुल सही उत्तर प्रकार6videos
JEE ADVANCED पेपर - 2 (2012)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )4videos
JEE ADVANCED पेपर - 2 (2014)
Similar Questions
माना कि S≠S1∩S2∩S3 , जहां S1={z∈C:|z|<4},S2={z∈CIm[z−1+√3i1−√3i]>0} तथा S3={z∈C:Rez>0}
minz∈S|1−3i−z|=07:05View Solutionसूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिए गए कोड का प्रयोग करके सही उत्तर चुनिये :
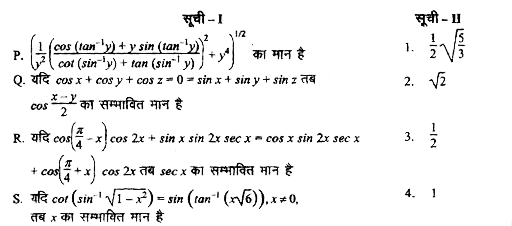 02:37View Solution
02:37View Solutionदो घटनायें X और Y इस प्रकार की हैं कि P(X∣Y)=12,P(Y∣X)=13 और P(XnY)=16 तब निम्न में से कौन कथन सही है/हैं?
06:47View Solutionइस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
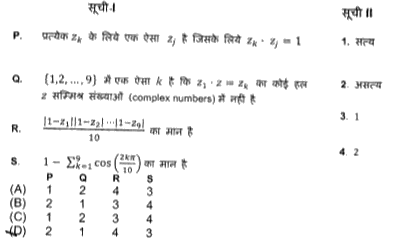 03:50View Solution
03:50View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
01:40View Solutionमाना A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है । यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1पर भ्रमण करता है तो शीर्ष C का बिन्दुपथ है -
03:14View Solutionमाना कि △PQR एक त्रिभुज है तथा →a=−−→QR,→b=−−→RP तथा →c=−−→PQ है | यदि |→a|=12,∣∣→b∣∣=4√3 तथा →b.→c=24 तो निम्न में से कोण-सा (से) सही है
04:32View Solutionमान A(2,−3) तथा B(−2,1) एक त्रिभुज ABC के शीर्ष है। यदि इस त्रिभुज का केन्द्रक सरल रेखा 2x+3y=1 पर भ्रमण करता है, तो शीर्ष C का बिन्दुपथ है:
06:20View Solutionवह वृत्त जो किसी त्रिभुज की सभी भुजाओं को बिना बढ़ाये स्पर्श करे कहलाता है:
05:59View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
02:42View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
03:50View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
49:09View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
34:41View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
04:14View Solutionयदि a तथा b इकाई सदिश हैं तथा θ इनके बीच का कोण है। तब ∣∣ˆa+ˆb∣∣<1 यदि
01:27View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
04:24View Solution

