माना कि a, r, s, t शून्येतर वास्तविक संख्यायें (non zero real numbers) हैं, P(at2,2at),Q,R(ar2,2ar) तथा S(as2,2as) परवलय y2=4ax पर स्थित विभिन्न बिन्दु हैं। माना कि PQ नाभीय जीवा (focal chord) है एवम् रेखायें QR तथा PK समानान्तर हैं, जहाँ K बिन्दु (2a,0) है।
r का मान है
−1t
t2+1t
1t
t2−1t
Step by step video & image solution for माना कि a, r, s, t शून्येतर वास्तविक संख्यायें (non zero real numbers) हैं, P(at^2, 2at), Q, R(ar^2, 2ar)" तथा "S(as^2, 2as) परवलय y^2 = 4ax पर स्थित विभिन्न बिन्दु हैं। माना कि PQ नाभीय जीवा (focal chord) है एवम् रेखायें QR तथा PK समानान्तर हैं, जहाँ K बिन्दु (2a,0) है। r का मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )4videos
JEE ADVANCED पेपर - 2 (2014)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )4videos
JEE ADVANCED पेपर - 2 (2014)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2013)EXERCISE - PART III : MATHEMATICS (खण्ड - 3) (सुमेलन सूची प्रकार)4videos
JEE ADVANCED पेपर - 2 (2013)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 3)4videos
JEE ADVANCED पेपर - 2 (2015)
Similar Questions
इस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
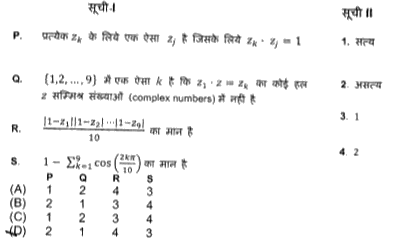 05:03View Solution
05:03View Solutionइस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
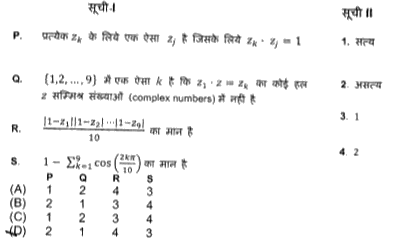 View Solution
View Solutionसूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिए गए कोड का प्रयोग करके सही उत्तर चुनिये :
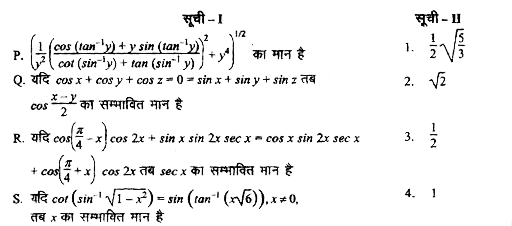 View Solution
View Solutionमाना कि बॉक्स I में n1 लाल गेंद और n2 काली गेंद हैं । माना कि बॉक्स II में n3 लाल गेंद और n4 काली गेंद हैं ।
बॉक्स I और बॉक्स II में से, यादृच्चया (at random) एक बॉक्स को चुना गया और इस चुने हुए बॉक्स से, यादृच्चया एक गेंद निकाली गयी । यह गेंद लाल रंग की पाई गयी । यदि इस लाल गेंद के बॉक्स II से निकाले जाने की प्रायिकता 13 है, तब निम्नलिखित में से n1,n2,n3 और n4 के सही संभव मान है (हैं)03:08View SolutionLet a, r, s, t be non-zero real numbers. Let P(at2,2at),Q,R(ar2,2ar)andS(as2,2as) be distinct points onthe parabola y2=4ax. Suppose that PQ is the focal chord and lines QR and PK are parallel, where K isthe point (2a, 0). The value of r is
07:05View SolutionLet a,r,s,t be non-zero real numbers. Let P (at2,2at),QR(ar2,2ar) and S (as2,2as) be distinct point on the parabola y2=4ax. Suppose the PQ si the focal chord and line QR and PK are parallel, where K is point (2a, 0)
It st = 1, then the tangent at P and the normal at S to the parabola meet at a point whose ordinate is04:35View Solutionमाना a,r,s,t शून्यक वास्तविक सख्याए है , माना P(at2,2at)Q,R(ar2,2ar) व S(as2,2as) परवलय y2=4ax पर बिन्दु हो व यदि PQ नाभीय जीवा हो एव रेखाये QR व PK समान्तर हो जहाँ k=(2a,0) तब दर्शाइये की r=t2−1t∣∣∣
05:05View Solutionमाना a,b,c वास्तविक संख्याएं है। माना x,y,z ऐसी वास्तविक संख्या है जो कभी शून्य नहीं हैं तथा x=cy+bz,y=az+cx तथा z=bx+ay, तो a2+b2+c2+2abc का मान है:
07:49View SolutionLet P(at2,2at),Q,R(ar2,2ar) be three points on a parabola y2=4ax. If PQ is the focal chord and PK, QR are parallel where the coordinates of k is (2a,0), then the value of r is
03:39View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
05:37View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
01:55View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
01:02View Solutionमाना कि a,r, s, t शून्येतर वास्तविक संख्याये (non zero real numbers) हैं, P(at2,2at),Q,R(ar2,2ar) तथा S(as2,2as) परवलय y2=4ax पर स्थित विभिन्न बिन्दु है। माना PQ नाभीय जीवा (focal chord) है एवम् रेखायें QR तथा PK समानान्तर हैं, जहाँ K बिन्दु (2a,0) है।
r का मान है:02:45View Solutionमाना कि a,r, s, t शून्येतर वास्तविक संख्याये (non zero real numbers) है, P(at2,2at),Q,R(ar2,2ar) तथा S(as2,2as) परवलय y2=4ax पर स्थित विभिन्न बिन्दु है। माना PQ नाभीय जीवा (focal chord) है एवम् रेखायें QR तथा PK समानान्तर है, जहाँ K बिन्दु (2a, 0) है।
यदि st = 1 है, तो इस परवलय के बिन्दु P पर स्पर्श रेखा तथा बिन्दु S पर अभिलम्ब (nomal) जिस बिन्दु पर मिलते है, उसकी कोटि (ordinate) है: (i) (t2+1)22t3 (ii) a(t2+1)22t3 (iii) a(t2+1)2t3 (iv) a(t2+2)2t305:37View Solutionपरवलय y2=36x पर स्थित वे बिन्दु जिनकी कोटि भुज की तिगुनी है, हैं
06:18View Solutionमाना की R कोई वास्तविक सँख्या का समुच्चय है। एक सक्रिया R पर इस प्रकार परिभाषित है कि a*b=a+b+2ab तो 2*3 का मान ज्ञात किया।
06:22View Solution

