माना कि एक समान्तर श्रेणी (arithmetic progression (A.P.)) के सभी पद धन पूर्णांक हैं । इस समान्तर श्रेणी में यदि पहले सात (7) पदों के योग और पहले ग्यारह (11) पदों के योग का अनुपात 6 : 11 है तथा सातवा पद 130 और 140 के बीच में स्थित है, तब इस समान्तर श्रेणी के सार्व अन्तर (common difference) का मान है
Step by step video solution for माना कि एक समान्तर श्रेणी (arithmetic progression (A.P.)) के सभी पद धन पूर्णांक हैं । इस समान्तर श्रेणी में यदि पहले सात (7) पदों के योग और पहले ग्यारह (11) पदों के योग का अनुपात 6 : 11 है तथा सातवा पद 130 और 140 के बीच में स्थित है, तब इस समान्तर श्रेणी के सार्व अन्तर (common difference) का मान है by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 2)8videos
JEE ADVANCED पेपर - 2 (2015)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग III : गणित (खंड - 3)4videos
JEE ADVANCED पेपर - 2 (2015)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART III : MATHEMATICS (खण्ड - 3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही) )4videos
JEE ADVANCED पेपर - 2 (2014)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- III गणित (खंड-3)4videos
JEE ADVANCED पेपर - 2 (2016)
Similar Questions
माना कि सभी x∈(−π2,π2) के लिए, f(x)=7tan8x+7tan6x−3tan4x−3tan2x है, तब सही कथन है (हैं)
01:53View Solutionमाना कि बॉक्स I में n1 लाल गेंद और n2 काली गेंद हैं । माना कि बॉक्स II में n3 लाल गेंद और n4 काली गेंद हैं ।
बॉक्स I और बॉक्स II में से, यादृच्चया (at random) एक बॉक्स को चुना गया और इस चुने हुए बॉक्स से, यादृच्चया एक गेंद निकाली गयी । यह गेंद लाल रंग की पाई गयी । यदि इस लाल गेंद के बॉक्स II से निकाले जाने की प्रायिकता 13 है, तब निम्नलिखित में से n1,n2,n3 और n4 के सही संभव मान है (हैं)03:49View Solutionइस खंड में 4 बहुविकल्पीय प्रश्न है। प्रत्येक प्रश्न में दो सुमेलन सूचियां है। सूचियों के लिए कूट के विकल्प और है जिनमें से केवल एक सही है।
माना की zk=cos(2kπ10)+isin(2kπ10),k=1,2,…,9
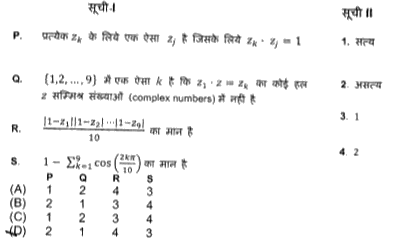 49:30View Solution
49:30View Solutionअनुच्छेद
फुटबॉल दलों T1 और T2 को एक दूसरे के विरुद्ध दो खेल (games) खेलने हैं। यह मान लिया गया है कि दोनों खेलों के परिणाम
एक दूसरे पर निर्भर नहीं करते। दल T1 के दल T2 के विरुद्ध एक खेल में जीतने, बराबर होने और हारने की प्रायिकता क्रमशः 12,16
और 13 हैं। प्रत्येक दल जीतने पर 3 अंक, बराबरी पर 1 अंक और हारने पर 0 अंक अर्जित करता है। माना कि दो खेलों के पश्चात दल
T1 और दल T2 के द्वारा अर्जित कुल अंक क्रमशः X और Y हैं।
P(X>Y) का मान है53:06View Solutionएक श्रेणी जिसका n वा पद nx+y है के r पदों का योगफल होगा
02:23View Solution(1+x)n के प्रसार में 9वे और 7वें पदों के गुणांकों का अनुपात 9:7 है। तब, 4वें पद (4th term) का गुणांक (coefficient) है
45:17View Solutionसमांतर श्रेणी | समांतर श्रेणी का व्यापक पद | समांतर श्रेणी के N पदों का योगफल | उदाहरण
55:33View Solutionगुणोत्तर श्रेणी | गुणोत्तर श्रेणी का व्यापक पद | गुणोत्तर श्रेणी के N पदों का योगफल | उदाहरण
33:07View Solutionएक श्रेणी, जिसका n वाँ पद (nx)+y है, तब r पदों का योग होगा
59:23View Solutionसमांतर श्रेणी के प्रथम N पदों का योग
57:46View Solutionगुणोत्तर श्रेणी के n पदों का योग|उदाहरण
View SolutionBoards 2021|समान्तर श्रेणी#!#A.P के प्रथम n पदों का क्षेत्रफल#!#Revision
50:53View Solutionअनंत गुणोत्तर श्रेणी के n पदों का योग|उदाहरण
57:45View Solutionगुणोत्तर श्रेणी के अनंत पदों का योग
51:22View SolutionRevision|समांतर श्रेणी का n वां पद#!#समांतर श्रेणी के n पदों का योग
40:12View SolutionRevision|समांतर श्रेणी के n पदों का योग
46:17View Solution

