क्षेत्र R={{x,y)∈R×R:x≥0 तथा y2=4−x } पर विचार कीजिए। माना F उन सभी वृत्तों का कुल है जो R में स्थित हैं तथा जिनके केंद्र x-अक्ष पर हैं। माना C वह वृत्त है जिसकी F के वृत्तों में से सबसे बड़ी त्रिज्या है। माना (α,β) एक बिंदु है जहाँ वृत्त C वक्र y2=4−x से मिलता है।
α का मान ______ है
The correct Answer is:2.00
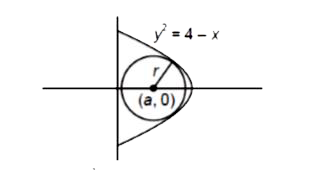
माना वृत्त है,
(x−a)2+y2=r2
इसे परवलय
y2=4−x के साथ हल करने पर
(x−a)2+4−x=r2
⇒x2−x(2a+1)+(a+4−2)=0....(1)
D = 0
⇒4r2+4a−15=0
स्पष्टत: a≥r
अतः 4r2+4r−15≤0
⇒rmax=32=a
वृत्त C की त्रिज्या 32 है
समीकरण (1) से x2−4x+4=0=x=0
⇒x=2=α
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2021)EXERCISE - MATHEMATICS (खंड-3)4videos
JEE ADVANCED पेपर - 2 (2021)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2021)EXERCISE - MATHEMATICS (खंड-4)3videos
JEE ADVANCED पेपर - 2 (2021)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2021)EXERCISE - MATHEMATICS (खंड-4)3videos
JEE ADVANCED पेपर - 2 (2021)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- III गणित (खंड-3)4videos
JEE ADVANCED पेपर - 2 (2016)
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सॉल्वड पेपर 2019EXERCISE - पेपर 2 खण्ड 34videos
JEE ADVANCED सॉल्वड पेपर 2019
Similar Questions
माना M={(x,y)R×R:x2+y2<r2), जहाँ r>0 है। गुणोत्तर श्रेणी an=12n−1,n=1,2,3, .... पर विचार कीजिए। माना S = 0 तथा n≥1 के लिए, माना Sn इस श्रेणी के प्रथम n पदों के योगफल को निरूपित करता है। n≥1 के लिए माना Cn उस वृत्त को निरूपित करता है जिसका केंद्र (Sn−1,0) है तथा त्रिज्या an है तथा Dn उस वृत्त को निरूपित करता है जिसका केंद्र (Sn−1,Sn−1) तथा त्रिज्या an है।
M पर विचार कीजिए जहाँ r=1025513 है। माना k उन सभी वृत्तों Cn की संख्या है जो M के अंदर स्थित हैं। माना l इन k वृत्तों में से उन वृत्तों की अधिकतम संभावित संख्या है जिसमें कोई दो वृत्त प्रतिच्छेद नहीं करते हैं। तब03:29View Solutionसमुच्चय {1, 2, 3......, 2000} में से एक संख्या का यादृच्छया चयन किया जाता है। माना चयनित संख्या के 3 या 7 का गुणज होने की प्रायिकता p है। तब 500p का मान ______ है |
03:14View Solutionसमुच्चय {1, 2, 3......, 2000} में से एक संख्या का यादृच्छया चयन किया जाता है। माना चयनित संख्या के 3 या 7 का गुणज होने की प्रायिकता p है। तब 500p का मान ______ है |
03:08View Solutionअनुच्छेद
फुटबॉल दलों T1 और T2 को एक दूसरे के विरुद्ध दो खेल (games) खेलने हैं। यह मान लिया गया है कि दोनों खेलों के परिणाम
एक दूसरे पर निर्भर नहीं करते। दल T1 के दल T2 के विरुद्ध एक खेल में जीतने, बराबर होने और हारने की प्रायिकता क्रमशः 12,16
और 13 हैं। प्रत्येक दल जीतने पर 3 अंक, बराबरी पर 1 अंक और हारने पर 0 अंक अर्जित करता है। माना कि दो खेलों के पश्चात दल
T1 और दल T2 के द्वारा अर्जित कुल अंक क्रमशः X और Y हैं।
P(X>Y) का मान है02:05View Solutionमाना कि f(x)=sin(πcosx)तथाg(x)=cos(2πsinx) दो फलन हैं जो x>0 में परिभाषित हैं | निम्नलिखित समुच्चय जिनके अवयवों को बढ़ते हुए क्रम (आरोही) में लिखा गया है, इस प्रकार परिभाषित हैं |
X={x:f(x)=0},Y={x:f'(x)=0}
Z={x:g(x)=0},W={x:g'(x)=0}
सूची-I में X, Y, Z और W समुच्चय हैं | सूची-II में इन समुच्चयों के बारे में कुछ सूचनाएं हैं |
सूची −I सूची−II
(I)X (P)⊇{π2,3π6,4π,7π}
(II)Y (Q) समांतर श्रेणी
(III)Z (R) समांतर श्रेणी नहीं है
(IV) W(S)⊇{π6,7π6,13π6}(T)⊇{π3,2π3,π}(U)⊇{π6,3π6}
निम्न में से कौन सा एक मात्र संयोजन सही है07:40View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
04:35View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
05:05View Solutionमाना a,b,c वास्तविक संख्याएं है। माना x,y,z ऐसी वास्तविक संख्या है जो कभी शून्य नहीं हैं तथा x=cy+bz,y=az+cx तथा z=bx+ay, तो a2+b2+c2+2abc का मान है:
06:54View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
02:29View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
04:37View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
03:52View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
03:50View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
04:26View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
05:20View Solutionवक्र y=xex2 की वह स्पर्श रेख जो बिंदु (1,e) से होकर जाती है, निम्न में से किस बिंदु से भी होकर जाती है ?
05:40View Solutionरेखा x−42=y−52=z−31 तथा समतल x+y+z=2 का प्रतिच्छेदन बिंदु निम्न में से किस रेखा पर स्थित है ?
05:40View Solution
