किसी वास्तविक संख्या x के लिए, माना [x], x के बराबर या इससे कम महत्तम पूर्णांक को निरूपित करता है। यदि I=∫100[√10xx+1]dx तब 9I का मान _____ है
The correct Answer is:182.00
I=∫100[√10xx+1]dx
y=10xx+1,0≤x≤10
xy+y=10x
x=y10−y
0≤y10−y≤10
y10−y≥0 तथा y10−y−10≤0
y10−y≤0 तथा 11y−100y−10≥0
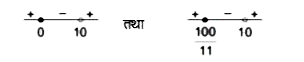
y∈[0,10) तथा y∈(−∞,10011]∪(10,∞)
y∈[0,10011]
√y∈[0,10√11]⇒[√y]={0,1,2,3}
स्थिति I : 0≤10xx+1<1
10xx+1≥0 तथा 10xx+1−1<0
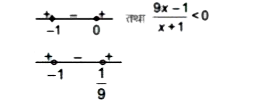
x∈(−∞,−1)∪[0,∞) तथा x∈(−1,19)
x∈[0,19) तब [√10xx+1]=0
स्थिति II : 4≤10xx+1<9
10xx+1−4≥0 तथा 10xx+1<9
6x−4x+1>0 तथा 10xx+1<9
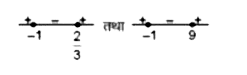
x∈(−∞,−1)∪[23,∞),x∈(−1,9)
x∈[23,9),[√10xx+1]=2
स्थिति IV : x∈[9,10]⇒[√10xx+1]=3
I=∫1900.dx+∫23191.dx+∫9232.dx+∫1093.dx
I=(23−19)+2(9−23)+3(10−9)
I=59+503+3
9I = 182
Topper's Solved these Questions
- JEE ADVANCED पेपर - 2 (2021)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2021)EXERCISE - MATHEMATICS (खंड-3)
4 Videos
- JEE ADVANCED पेपर - 2 (2016)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- III गणित (खंड-3)
4 Videos
- JEE ADVANCED सॉल्वड पेपर 2019BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED सॉल्वड पेपर 2019EXERCISE - पेपर 2 खण्ड 3
4 Videos
Similar Questions
माना M={(x,y)R×R:x2+y2<r2), जहाँ r>0 है। गुणोत्तर श्रेणी an=12n−1,n=1,2,3, .... पर विचार कीजिए। माना S = 0 तथा n≥1 के लिए, माना Sn इस श्रेणी के प्रथम n पदों के योगफल को निरूपित करता है। n≥1 के लिए माना Cn उस वृत्त को निरूपित करता है जिसका केंद्र (Sn−1,0) है तथा त्रिज्या an है तथा Dn उस वृत्त को निरूपित करता है जिसका केंद्र (Sn−1,Sn−1) तथा त्रिज्या an है।
M पर विचार कीजिए जहाँ r=1025513 है। माना k उन सभी वृत्तों Cn की संख्या है जो M के अंदर स्थित हैं। माना l इन k वृत्तों में से उन वृत्तों की अधिकतम संभावित संख्या है जिसमें कोई दो वृत्त प्रतिच्छेद नहीं करते हैं। तब
View Solutionअनुच्छेद
फुटबॉल दलों T1 और T2 को एक दूसरे के विरुद्ध दो खेल (games) खेलने हैं। यह मान लिया गया है कि दोनों खेलों के परिणाम
एक दूसरे पर निर्भर नहीं करते। दल T1 के दल T2 के विरुद्ध एक खेल में जीतने, बराबर होने और हारने की प्रायिकता क्रमशः 12,16
और 13 हैं। प्रत्येक दल जीतने पर 3 अंक, बराबरी पर 1 अंक और हारने पर 0 अंक अर्जित करता है। माना कि दो खेलों के पश्चात दल
T1 और दल T2 के द्वारा अर्जित कुल अंक क्रमशः X और Y हैं।
P(X>Y) का मान है
View Solutionमाना कि f(x)=sin(πcosx)तथाg(x)=cos(2πsinx) दो फलन हैं जो x>0 में परिभाषित हैं | निम्नलिखित समुच्चय जिनके अवयवों को बढ़ते हुए क्रम (आरोही) में लिखा गया है, इस प्रकार परिभाषित हैं |
X={x:f(x)=0},Y={x:f'(x)=0}
Z={x:g(x)=0},W={x:g'(x)=0}
सूची-I में X, Y, Z और W समुच्चय हैं | सूची-II में इन समुच्चयों के बारे में कुछ सूचनाएं हैं |
सूची −I सूची−II
(I)X (P)⊇{π2,3π6,4π,7π}
(II)Y (Q) समांतर श्रेणी
(III)Z (R) समांतर श्रेणी नहीं है
(IV) W(S)⊇{π6,7π6,13π6}(T)⊇{π3,2π3,π}(U)⊇{π6,3π6}
निम्न में से कौन सा एक मात्र संयोजन सही है
View Solutionयदि किसी समीकरण के प्रत्येक पद मे x एक सर्वनिष्ठ खंड है तब x का मान सदैव होगा-
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionयदि A=[logx−1−logx2] और यदि det (A)=2, तब x का मान है
View Solutionयदि A=[axya] और यदि xy=1, तब det(AAT) के बराबर है
View Solutionवास्तविक संख्या x के लिए संतुष्ट के लिए, x2−|x+2|+x>0 होगा?
View Solutionयदि x∈(0,14) के लिए tan−1(6x√x1−9x3) का अवकलन √x.g(x) है, तो g(x) बराबर है
View Solutionमाना z∈C जिसके लिए Im (z) = 10 तथा किसी प्राकृत संख्या n के लिए यह 2z−n2z+n=2i−1 को संतुष्ट करता है , तो
View Solutionयदि (1+xlog2x)5 के द्विपद प्रसार में तीसरा पद 2560 के बराबर है, तो x का एक सम्भव मान है
View Solution∫π/2−π/2dx[x]+[sinx]+4 का मान है [जहाँ t] वह महत्तम पूर्णांक है जो t से कम या बराबर है|
View Solutionसमाकल 2∫−2sin2x[xπ]+12dx (जहाँ [x], x के समान या उससे कम महत्तम पूर्णांक को दर्शाता है ) का मान है
View Solutionमाना [x], x के समान या उसे कम महत्तम पूर्णांक को दर्शाता है , तो limx→0tan(πsin2x)+(|x|−sin(x[x]))2x2
View Solution3cosθ+5sin(θ−π6) का θ के किसी भी वास्तविक मान के लिए अधिकतम मान है
View Solutionमाना m ऐसा न्यूनतम धनात्मक पूर्णांक है की (1+x)2+(1+x)3+........+(1+x)49+(1+xm)50 के विस्तार में x2 का गुणांक (3n+1)51C3 किसी धनात्मक पूर्णांक n के लिए तब, n का मान है
View Solution
