एक समांतर पट्टिका संधारित्र की पट्टिकाओं का क्षेत्रफल S तथा पट्टिकाओं के बीच में दूरी d है । तथा इसकी वायु में धारिता C1 है। जब पट्टिकाओं के मध्य दो अलग-अलग सापेक्ष परावैद्युतांकों ( ε1=2 तथा ε2=4) के परावैद्युत पदार्थ दर्शाये चित्रानुसार रखे जाते हैं तब इस प्रकार बने नये संधारित्र की धारिता C2 हो जाती है । तब अनुपात C2C1 है
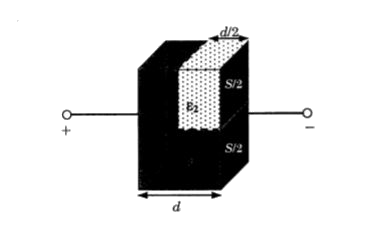
6/5
5/3
7/5
7/3
Step by step video & image solution for एक समांतर पट्टिका संधारित्र की पट्टिकाओं का क्षेत्रफल S तथा पट्टिकाओं के बीच में दूरी d है । तथा इसकी वायु में धारिता C_1 है। जब पट्टिकाओं के मध्य दो अलग-अलग सापेक्ष परावैद्युतांकों ( epsilon_1 = 2 तथा epsilon_2 = 4) के परावैद्युत पदार्थ दर्शाये चित्रानुसार रखे जाते हैं तब इस प्रकार बने नये संधारित्र की धारिता C_2 हो जाती है । तब अनुपात C_2/C_1 है by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग I : भौतिक विज्ञान (खंड - 3)
4 Videos
- JEE ADVANCED पेपर - 2 (2015)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2015)EXERCISE - भाग I : भौतिक विज्ञान (खंड- 2)
1 Videos
- JEE ADVANCED पेपर - 2 (2014)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2014)EXERCISE - PART I : PHYSICS (खण्ड -3 : सुमेलन सूची प्रकार (केवल एक विकल्प सही))
4 Videos
- JEE ADVANCED पेपर - 2 (2016)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - JEE ADVANCED पेपर - 2 (2016)EXERCISE - भाग- I भौतिक विज्ञान (खंड-3)
4 Videos
Similar Questions
दर्शाये चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा I धनात्मक x-दिशा में प्रवाहित हो रही है । पट्टी की लंबाई, चौड़ाई तथा मोटाई क्रमशः l, w तथा d हैं । पट्टी पर धनात्मक y-दिशा में एक एकसमान चुम्बकीय क्षेत्र →B लगाया गया है । इसके कारण आवेशवाहक z -दिशा की ओर विक्षेपित होते हैं । परिणामतः सतह PQRS पर आवेशवाहकों का संचयन होता है तथा PQRS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है । एक विभांतर z-दिशा के साथ इस प्रकार विकसित होता है । आवेश वाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से संतुलित नहीं हो जाता । विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है।
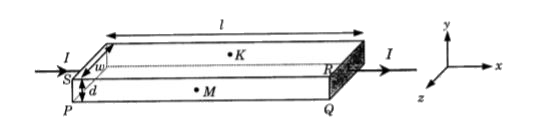
एक ही चालक (metallic) पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) को लें । उनकी लंबाईयाँ बराबर हैं, चौड़ाईयाँ क्रमशः w1 एवं w2 तथा मोटाईयाँ क्रमशः d1 तथा d2 हैं । दो बिन्दु K तथा M x-y तल के समांतर आमने-सामने के फलकों पर स्थित हैं। पट्टियों 1 तथा 2 में K तथा M के बीच विभवान्तर क्रमशः V1 तथा V2 हैं । तब उनमें बहने वाली एक दी गयी विद्युत धारा I तथा एक दी गयी चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
View Solutionएक एक-परमाणुक आदर्श गैस एक क्षौतिज बर्तन (horizontal cylinder) में स्प्रिंग-युक्त पिस्टन द्वारा बंद है (दर्शाये चित्रानुसार) । प्रारंभ में गैस का तापमान T1 दाब P1 तथा आयतन V1 है तथा स्प्रिंग विश्रांत अवस्था में है । अब गैस को बहुत धीरे-धीरे तापमान T2, तक गर्म करने पर दाब P2 तथा आयतन V2 हो जाता है । इस प्रक्रिया में पिस्टन x दूरी तय करता है । पिस्टन एवं बर्तन के मध्य घर्षण को नगण्य मानते हुए, सही कथन है (हैं)

View Solutionचार आवेश Q1,Q2,Q3 तथा Q4 जिनका मान समान है, x अक्ष के अनुदिश क्रमश: x=−2a,−a,+a तथा +2a पर रखे हुए हैं । एक अन्य धनावेश q, + y अक्ष पर b > 0 दूरी पर रखा है । आवेशों के चिह्न (sign) के चार विकल्प सूची-I में दिए हैं | आवेश q पर लगने वाले बलों की दिशा सूची-II में दी गई है । सूची-1 को सूची-II से सुमेलित कीजिए तथा सूचियों के नीचे दिये गए कोड का प्रयोग करके सही विकल्प चुनिए :
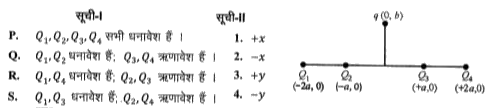
View Solutionअनुच्छेद 1
एक निर्देश तंत्र जो एक जड़त्वीय निर्देश तंत्र की तुलना में त्वरित हो, अजड़त्वीय निर्देश तंत्र कहलाता है। स्थिर कोणीय वेग ω से घूमती
हुई डिस्क पर बद्ध (fixed) निर्देश तंत्र अजड़त्वीय तंत्र का एक उदाहरण है। m द्रव्यमान का एक कण घूमती हुई डिस्क पर गतिमान है।
गतिमान कण डिस्क पर बद्ध निर्देश तंत्र के सापेक्ष बल →Frot तथा एक जड़त्वीय निर्देश तंत्र के सापेक्ष बल →Fin को महसूस करता है।
→Frot और →Fin के बीच का संबंध निम्नलिखित समीकरण में दिया गया है
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω,
यहाँ पर →vrot घूमते हुए निर्देश तंत्र में कण का वेग है तथा →r कण का डिस्क के मध्य बिन्दु के सापेक्ष स्थिति सदिश (position
vector) है।
मानिए कि R त्रिज्या की एक डिस्क, जिसमें व्यास के समानान्तर एक घर्षणरहित खाँचा है, एक स्थिर कोणीय गति ω से अपने अक्ष पर
वामावर्त दिशा में घूम रही है। एक निर्देश तंत्र मानिए जिसका मूलबिंदू डिस्क के मध्य बिन्दु पर है एवं x-अक्ष खाँचे के समानान्तर है,
y-अक्ष खाँचे के अभिलम्ब पर है एवं z-अक्ष घूमने वाली अक्ष के समानान्तर है (→ω=ωˆk)। m द्रव्यमान वाले एक छोटे गुटके को
समय t = 0 पर →r=(R/2)ˆi बिन्दु पर धीरे से इस तरह से रखा जाता है कि वो सिर्फ खाँचे में ही चल सके।
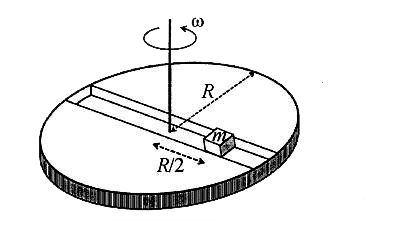
समय t पर गुटके की दूरी r का मान है:
View Solutionसंधारित्र तथा धारिता | समांतर पट्टिका संधारित्र
View Solutionसंधारित्र तथा धारिता | समांतर पट्टिका संधारित्र
View Solutionसमान्तर पट्टिका संधारित्र के प्लेटों के बीच परावैद्युत माध्यम
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionवैद्युत धारिता की अभिधारणा तथा इसकी परिभाषा | विलगित गोलीय चालक की धारिता | संधारित्र की धारिता
View Solutionसंधारित्र की धारिता पर परावैद्युत का प्रभाव | समान्तर-प्लेट संधारित्र की धारिता जब उसकी प्लेटों के बीच आंशिक रूप से परावैद्युत पदार्थ रखा हो
View Solutionचालक तथा संधारित्र की धारिता
View Solutionचालक तथा संधारित्र की धारिता
View SolutionRecap|समांतर प्लेट संधारित्र की धारिता जब प्लेटों के बीच परावैद्युत माध्यम भरा हो |OMR|Summary
View Solutionसमान्तर रेखाओं ax+by+c=0 तथा ax+by+d=0 के बीच की दुरी निकालें।
View Solutionयदि पिता एवं पुत्र की आयु का योग (वर्षो में) 65 है तथा उनकी आयु के अन्तर का दुगुना 50 वर्ष है तब पिता की आयु होगी -
View Solutionधारिता|संधारित्र का सिद्धांत|आवेशित संधारित्र में संचित ऊर्जा|गोलीय संधारित्र की धारिता|OMR|Summary
View Solution
