vector →a lies in the xy plane, has a magnitude of 18 units, and points in a direction 250∘ from the positive direction of the x axis. Also, vector →b has a magnitude of 12 units and points in the positive direction of the z axis. What is the vector product →c=→a×→b ?
30
35
40
45
The correct Answer is:D
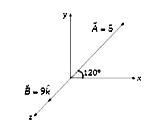
→A=(5cos120)ˆi+(5sin120)ˆj=−52ˆi+5√32ˆj
→B=9ˆk
→A×→B=∣∣
∣
∣∣ˆiˆjˆk−525√320009∣∣
∣
∣∣=−(−452)ˆj+(45√32)ˆi
→A×→B=45√32ˆi+452ˆj
∣∣→A×→B∣∣=
⎷(45√32)2+(452)2=452√4=45
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Lami.s Theorem)2videos
BASIC MATHEMATICS AND VECTORS
- BOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - Past Years Questions12videos
BASIC MATHEMATICS AND VECTORS
- BOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Addition and Subtraction of Vectors )34videos
BASIC MATHEMATICS AND VECTORS
- BOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON10videos
ELASTICITY
Similar Questions
Knowledge Check
- Question 1 - Select One
If a vector has an x-component of -250units and a y-component of 40.0 units, then the magnitude and direction of this vector is
A5√89 units, sin−1(5√89) with +ve-x-axisB5√89 units, cos−1(5√89) with -ve-x-axisC45 units, cos−1(−59) with x-axisD45 units, sin−1(−59) with x-axis - Question 2 - Select One
→A is a vector of magnitude 2.7 units due east . What is the magnitude and direction of vector 4 →A ?
A4 units due eastB4 units due westC2.7 units due eastD10.8 units due east - Question 3 - Select One
A vector of magnitude 14 lies in the xy-plane and makes an angle of 60∘ with x -axis . The components of the vector in the direction of x -axis and y-axis are
A7,7√3B7√3,7C14√3,14/√3D14/√3,14√3
Find a vector in the direction of vector 5ˆi−ˆj+2ˆk which has magnitude 8 units.
View SolutionVector →A has a magnitude of 6.00 vector →B has a magnitude of 7.00 units, and →A.→B has a value of 14.0 What is the angle between the direction of →Aand→B ?
View SolutionThere vectors →a,→b and →c each have a magnitude of 50 m and lie in an xy plane. Their directions relative to the positive direction of the x axis are 30∘,195∘,and315∘, respectively. What are (a) the magnitude and (b) the angle of the vector →a+→b+→c, and (c ) the magnitude and (d) the angle of →a−→b−→c ? What are the (e) magnitude and (f) angle of a fourth vector →d such that (→a+→b)−(→c+→d)=0 ?
View SolutionIf →A is a vector of magnitude 4 units due east. What is the magnitude and direction of a vector −4→A ?
View SolutionIf ¯¯¯A a vector of magnitude 5 units due east, what is the magnitude and direction of a vector ¯¯¯A ?
View Solution

