A uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is 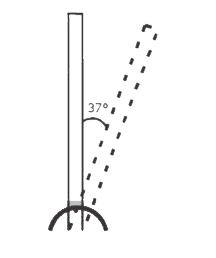
(gL)1/2
(3g4L)1/2
(3√3g2l)1/2
(3g2l)1/2
The correct Answer is:D
cos60∘=L2−ΔhL/2
⇒L2−Δh=L4
⇒Δh=L4
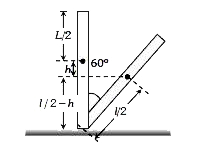
Decreases is PE= MgΔh=MgL4
K.E. of rotation =12Iω2=12.ML23ω2
⇒MgL4=ML26ω2
⇒ω2=6g4L⇒ω=√3g2L
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Rolling on Inclined Plane)54videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - PAST YEARS QUESTIONS70videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)52videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason15videos
SIMPLE HARMONIC MOTION
Similar Questions
Consider a uniform rod of mass M and length L is hinged at one end as shown. Initially the rod is vertical, it is slightly pushed and released. Find the angular velocity of rod and liner velocity of its one end when the rod becomes horizontal. Also calculate angular velocity of rod when it has rotated by an angle θ(θ<90∘).
View SolutionA thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View Solution
Knowledge Check
- Question 1 - Select One
A rod of length L, hinged at the bottom is held vertically and then allowed to fall, the linear velocity of its top when it hits the floor is
A√2gLB√2gLC√3gLD√3gL - Question 2 - Select One
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3g - Question 3 - Select One
A rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
A√2gLB√3gLC√g2LD√gL
A uniform rod of length 2a is held with one end resting on a smooth horizontal table making an angle a with the vertical. Show that when the rod is released, its angular velocity when it makes an angle θ with the vertical is given by
ω=[6g(cosα−cosθ)(1+3sin2α)]View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View SolutionA rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
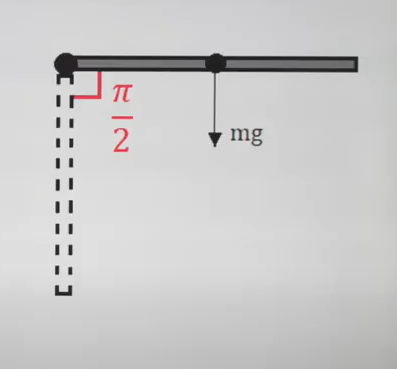 View Solution
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
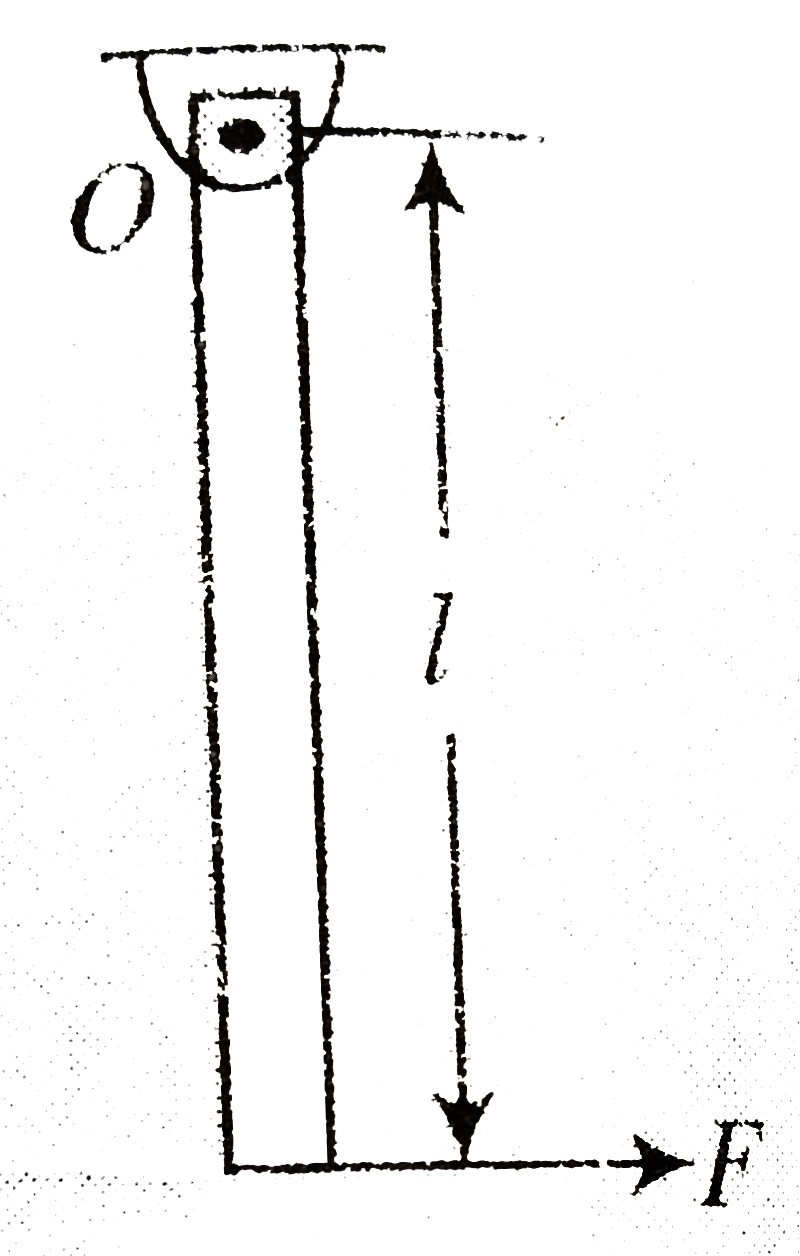 View Solution
View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, When it is in verticle position is
View Solution

