The change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2,T) is equal to
Zero
R In T
R In V1V2
R In V1V1
The correct Answer is:D
Change in entropy of an ideal gas -
ΔS=ΔQT
For isothermal process ΔU=0 Now, ΔQ=ΔU+ΔW⇒ΔQ=ΔW
ΔQ=ΔW=nRTIn(V2V1)
for n = 1 (one mole) ΔS=ΔQT=RIn(V2V1)
Topper's Solved these Questions
- THERMODYNAMICSBOOK - ERRORLESSCHAPTER - THERMODYNAMICSEXERCISE - PAST YEARS QUESTIONS
22 Videos
- THERMODYNAMICSBOOK - ERRORLESSCHAPTER - THERMODYNAMICSEXERCISE - ASSERTION AND REASON
20 Videos
- THERMODYNAMICSBOOK - ERRORLESSCHAPTER - THERMODYNAMICSEXERCISE - NCERT BASED QUESTIONS (ISOBARIC AND ISOCHORIC PROCESS)
10 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYBOOK - ERRORLESSCHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYEXERCISE - ASSERTION & REASON
10 Videos
Similar Questions
One mole of an ideal gas expands adiabatically from w an initial state (?A,?0) to final state (?_f, 5V_0).A¬hermo≤ofthesamegasexpandsisothermallyomad⇔erent∈itialstate(?B,?0)→thesamef∈alstate(?_f 5V_0).Theratioofthespecificheatsatconstantpressureandconstantvolumeofthisalgasisgamma.WˆistheratioT_A/T_B?
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
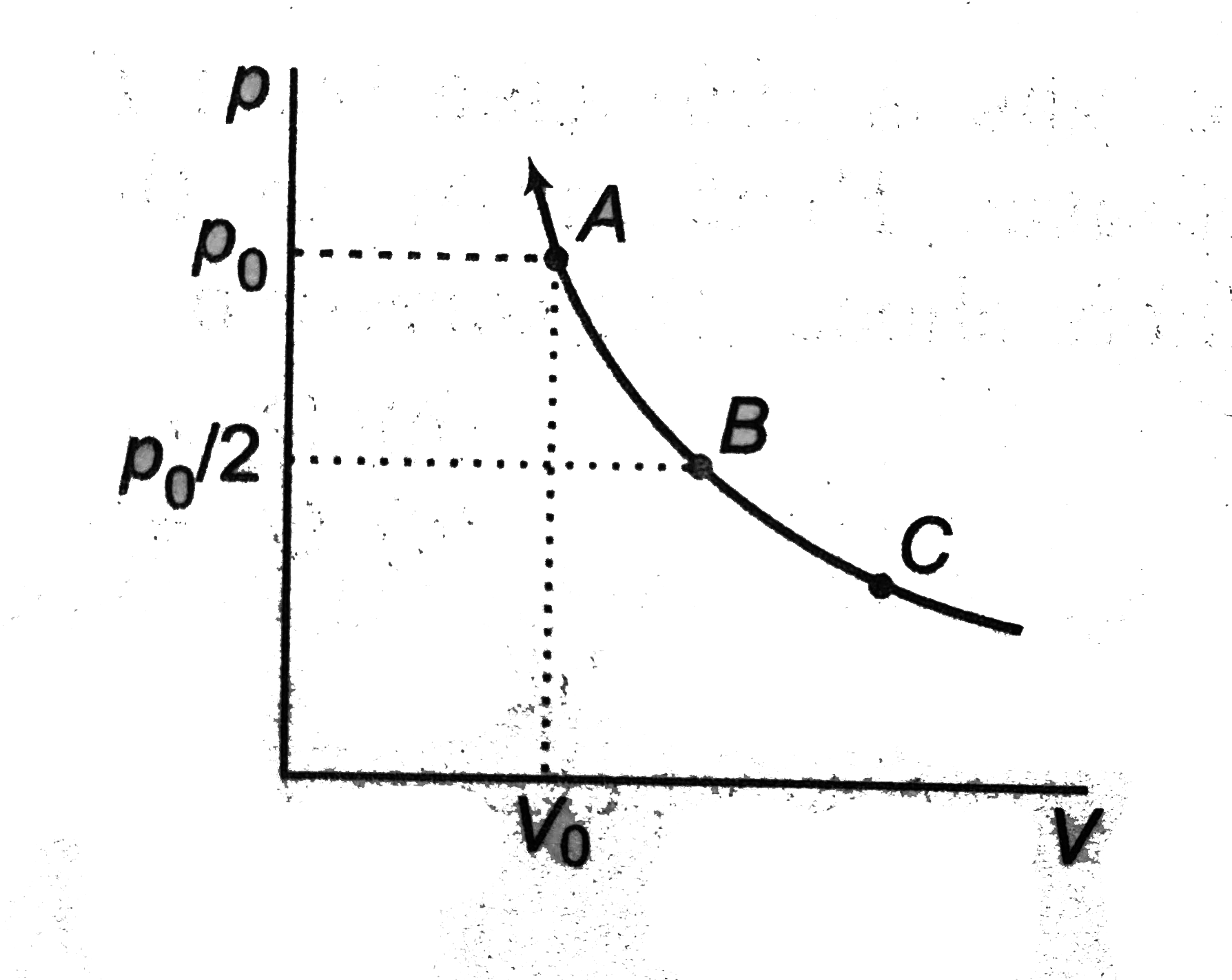
View Solution
Knowledge Check
The change in the entropy of a 1 mole of an ideal gas which went through an isothermal process form an initial state (P1,V1,T) to the final state (P2,V2<T) is equal to
AzeroBR ln TCR ln V1V2DRln(V2)V1One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
ACV(T1−T2)BCP(T1−T2)CCP+CV2(T1−T2)D(CP−CV)(T1−T2)When a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P-V curve, V-T curve,P-T curve etc.
For example, P-V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V-T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed.
Now, answer the following questions :
Two moles of an ideal gas is changed from its initial state (16 atm, 6L) to final state (4 atm, 15L) in such a way that this change can be represented by a straight line in P-V curve.The maximum temperature attained by the gas during the above change is :(Take : R=112LatmK−1mol−1)A324 KB648 KC1296 KD972 K
If n moles of an ideal gas are expanded is isothermally and reversibly from an initial state in which it has pressure p1 and volume V1 to the final state of volume V2 and pressure P2, then
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
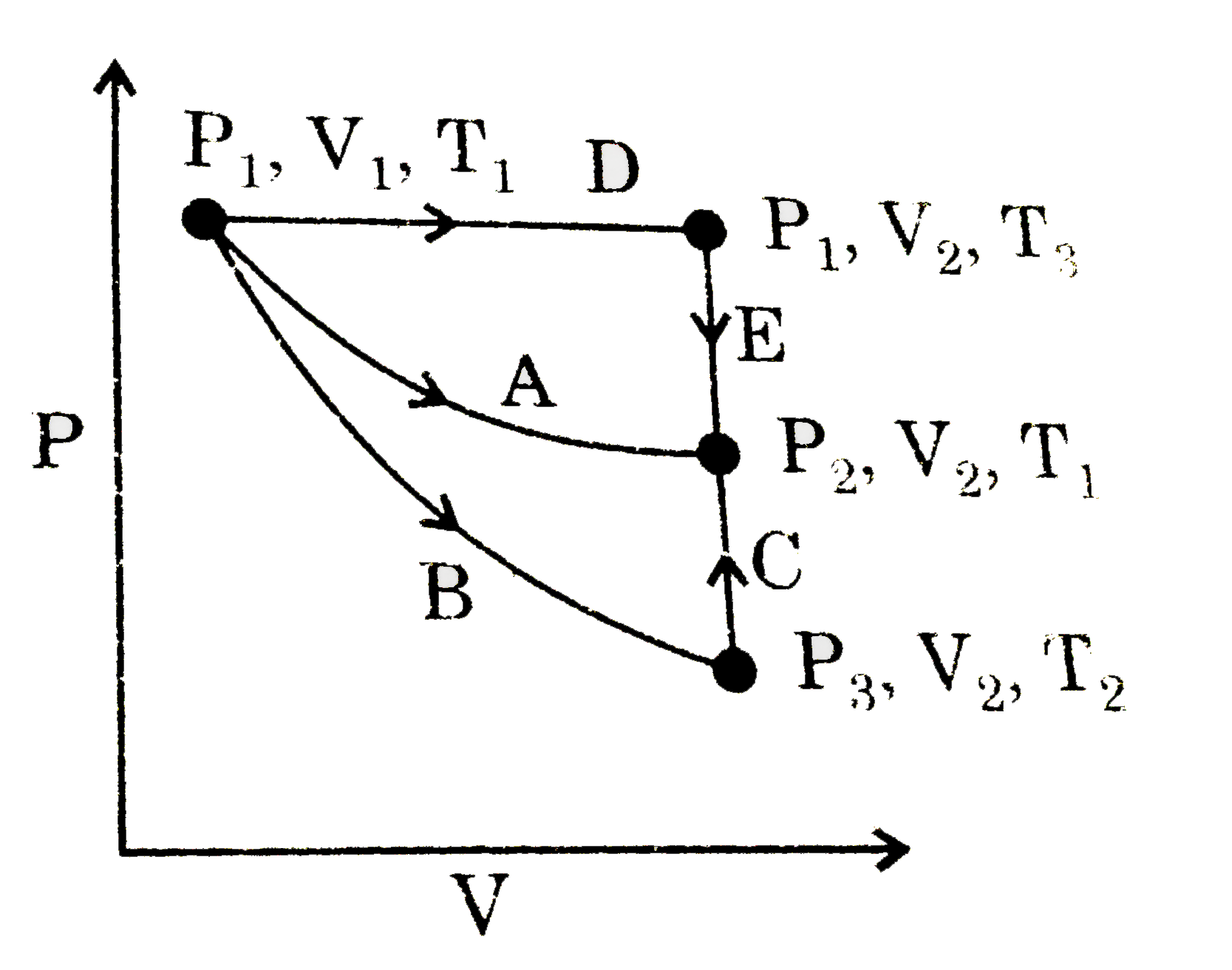
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is qrev for path (A)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
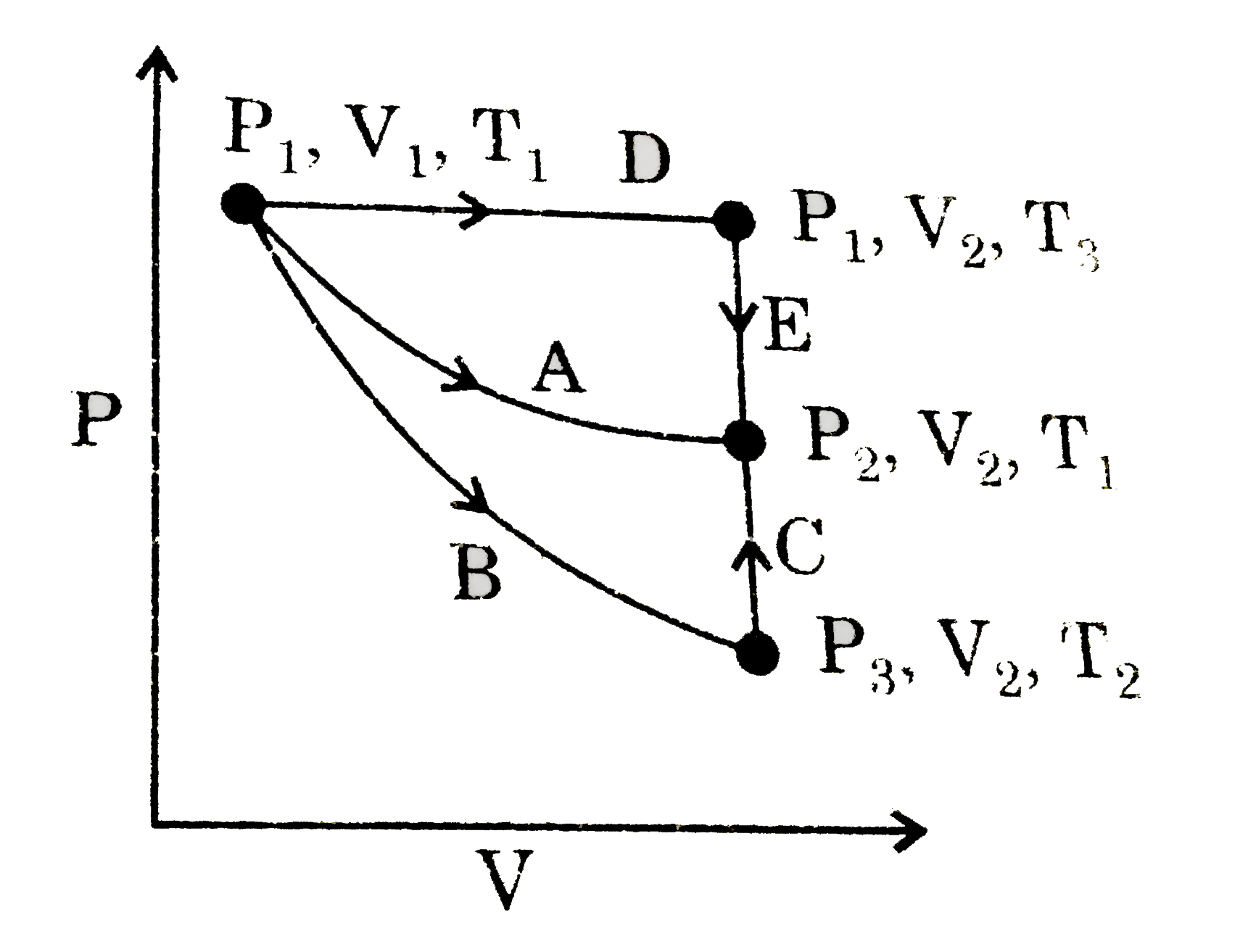
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for (D+E)?
View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure .
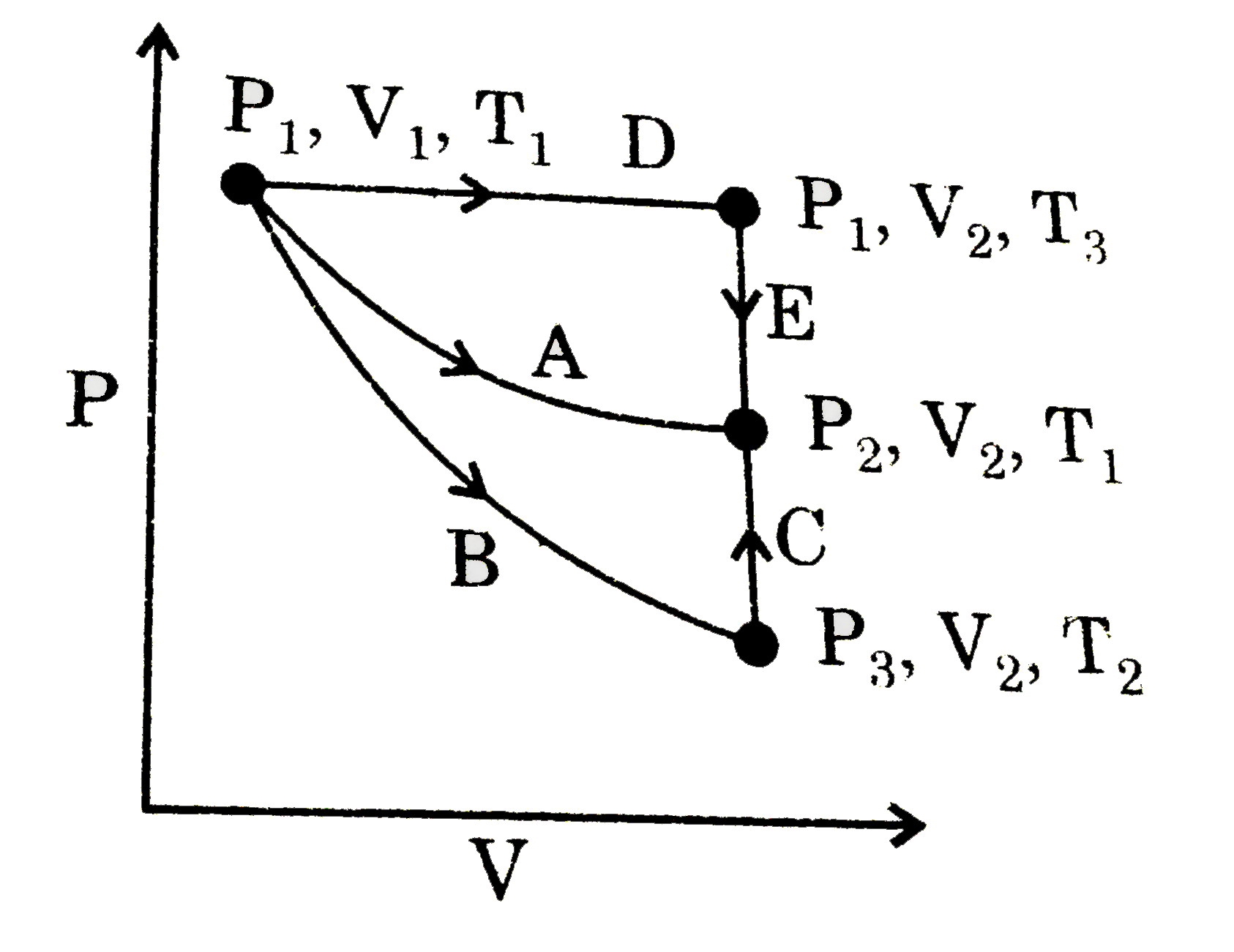
Path A represents a reversible isothermal from P1V1 to P2,V2, path (B+C) represent a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating of the gas at constant volume (C) from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) form P1,V2,T3 to P2,V2,T1
What is ΔS for path (A)?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
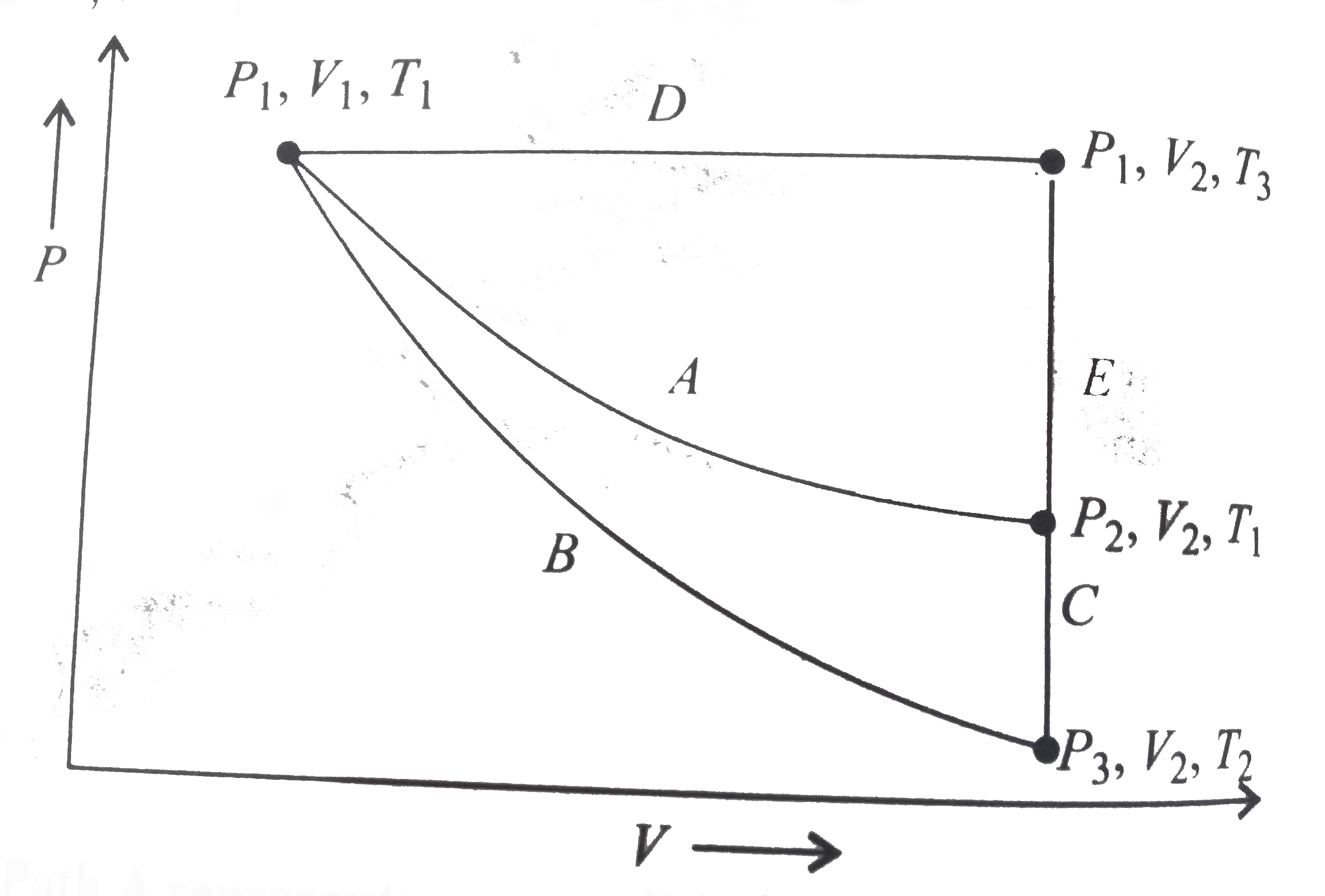
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?
View Solution
