A uniform rod of length L and mass M is held vertical, with its bottom end pivoted to the floor. The rod falls under gravity, freely turning about the pivot. If acceleration due to gravity is g, what is the instantaneous angular speed of the rod when it makes an angle 60∘ with the vertical
(gL)1/2
(3g4L)1/2
(3√3g2L)1/2
(3g2L)1/2
The correct Answer is:A
To solve the problem of finding the instantaneous angular speed of a uniform rod when it makes an angle of 60 degrees with the vertical, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Understand the Initial and Final States
Initially, the rod is vertical, and its center of mass is at a height of L2 from the pivot. When the rod falls and makes an angle of 60 degrees with the vertical, its center of mass is at a lower height.
Step 2: Calculate the Initial Potential Energy
The initial potential energy (PE_initial) of the rod when it is vertical can be calculated as:
PEinitial=Mg(L2)
Step 3: Calculate the Final Height of the Center of Mass
When the rod makes an angle of 60 degrees with the vertical, the height of the center of mass from the pivot is:
hfinal=L2cos(60∘)=L2⋅12=L4
Step 4: Calculate the Final Potential Energy
The final potential energy (PE_final) when the rod is at 60 degrees is:
PEfinal=Mg(L4)
Step 5: Set Up the Conservation of Energy Equation
According to the conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Since the rod starts from rest, KEinitial=0. Thus, we have:
Mg(L2)=Mg(L4)+12Iω2
where I is the moment of inertia of the rod about the pivot, which is given by:
I=13ML2
Step 6: Substitute the Moment of Inertia
Substituting I into the equation:
Mg(L2)=Mg(L4)+12(13ML2)ω2
Step 7: Simplify the Equation
Cancel M from all terms (assuming M≠0):
g(L2)=g(L4)+16L2ω2
Now, simplifying further:
g(L2−L4)=16L2ω2
g(L4)=16L2ω2
Step 8: Solve for Angular Speed ω
Rearranging gives:
ω2=6gL⋅L4
ω2=6g4=3g2
Taking the square root:
ω=√3g2
Final Answer
The instantaneous angular speed of the rod when it makes an angle of 60 degrees with the vertical is:
ω=√3g2
Initially, the rod is vertical, and its center of mass is at a height of L2 from the pivot. When the rod falls and makes an angle of 60 degrees with the vertical, its center of mass is at a lower height.
The initial potential energy (PE_initial) of the rod when it is vertical can be calculated as:
PEinitial=Mg(L2)
When the rod makes an angle of 60 degrees with the vertical, the height of the center of mass from the pivot is:
hfinal=L2cos(60∘)=L2⋅12=L4
The final potential energy (PE_final) when the rod is at 60 degrees is:
PEfinal=Mg(L4)
According to the conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Since the rod starts from rest, KEinitial=0. Thus, we have:
Mg(L2)=Mg(L4)+12Iω2
where I is the moment of inertia of the rod about the pivot, which is given by:
I=13ML2
Substituting I into the equation:
Mg(L2)=Mg(L4)+12(13ML2)ω2
Cancel M from all terms (assuming M≠0):
g(L2)=g(L4)+16L2ω2
Now, simplifying further:
g(L2−L4)=16L2ω2
g(L4)=16L2ω2
Rearranging gives:
ω2=6gL⋅L4
ω2=6g4=3g2
Taking the square root:
ω=√3g2
The instantaneous angular speed of the rod when it makes an angle of 60 degrees with the vertical is:
ω=√3g2
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Rolling on Inclined Plane)54videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - PAST YEARS QUESTIONS70videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)52videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason15videos
SIMPLE HARMONIC MOTION
Similar Questions
A uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
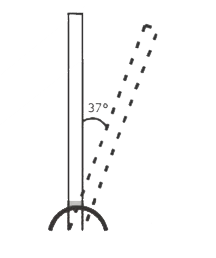 View Solution
View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View Solution
Knowledge Check
- Question 1 - Select One
A slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
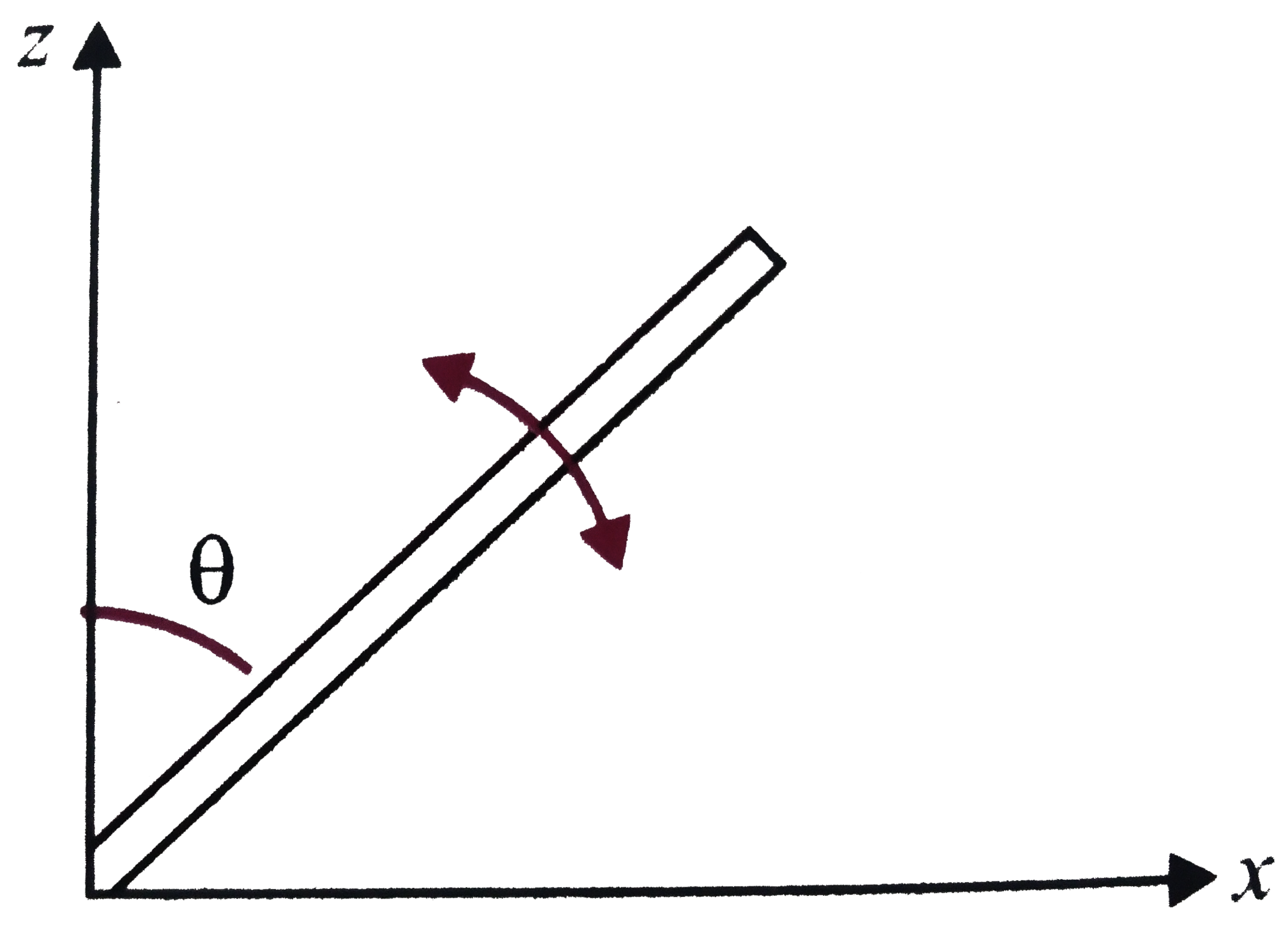 A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθ
A3g2lcosθB2g3lcosθC3g2lsinθD2g3lsinθ - Question 2 - Select One or More
A thin and uniform rod of mass M and length L is held vertical on floor with large friction. The rod is released from rest so that is falls by rotating about is contact-point with the floor without slipping. Which of the following statement(s) si/are correct. When the rod makes an angle 60∘ with vertical? [g is the acceleration due to gravity]
AThe Normal reaction force from the floor on the rod will be Mg16BThe angular acceleration of the rod will be 2gLCThe angular speed of the rod will be √3g2LDThe radial acceleration of the rod's center of mass will be 3g4 - Question 3 - Select One or More
A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is(are) correct, when the rod makes an angle 60° with vertical? [g is the acceleration due to gravity]
AThe normal reaction force from the floor on the rod will be Mg16BThe angular acceleration of the rod will be 2gLCThe radial acceleration of the rod’s center of mass will be 3g4DThe angular speed of the rod will be √3g2L
A uniform rod of length L and mass M is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
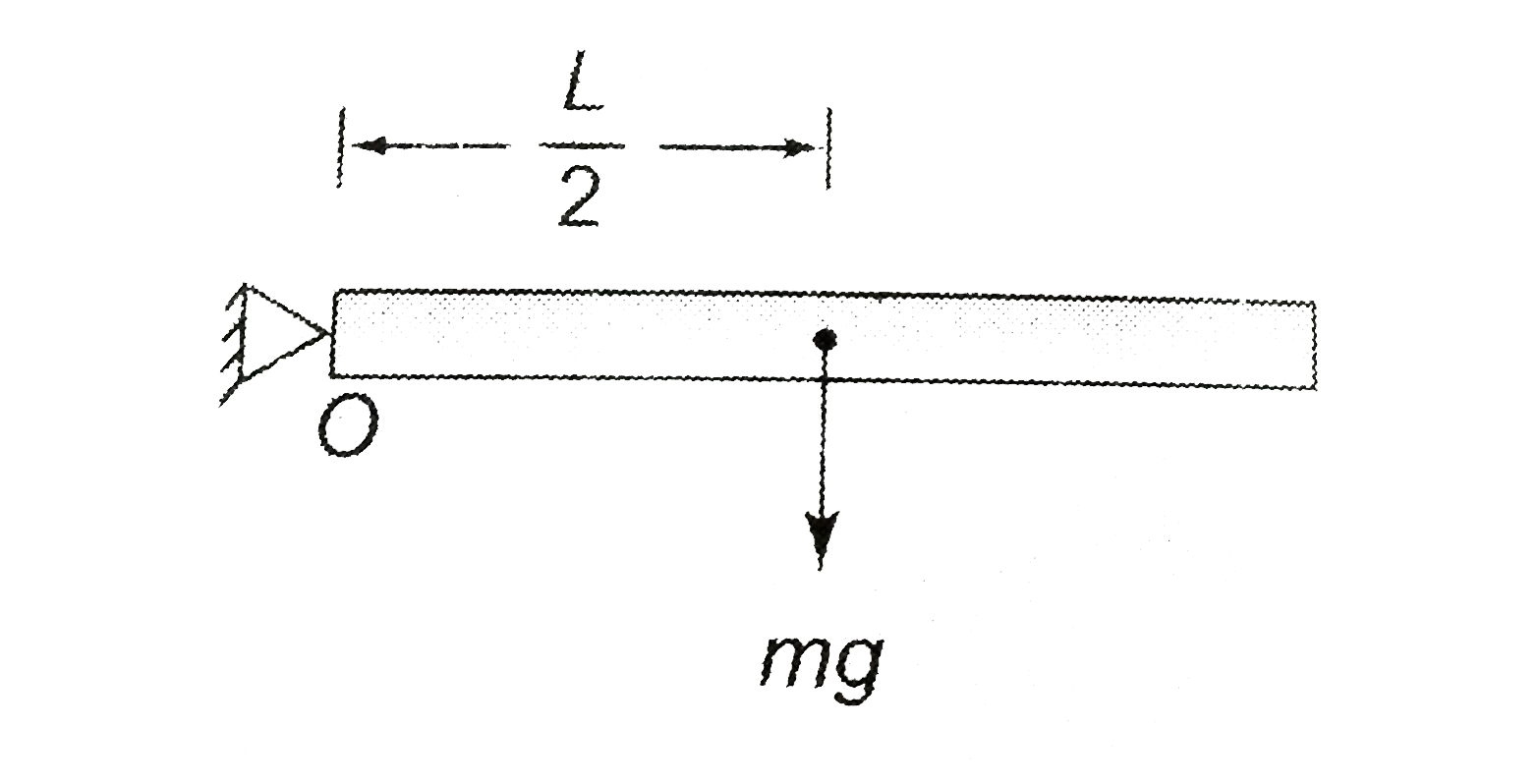 View Solution
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
 View Solution
View SolutionA uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.View SolutionA uniform rod of length l is from rest such that it rotates about a smooth pivot. The angular speed of the rod when it becomes vertical is.
 .View Solution
.View SolutionA rod of length L, hinged at the bottom is held vertically and then allowed to fall, the linear velocity of its top when it hits the floor is
View Solution

