A wheel is rolling along the ground with a speed of 2ms−1 The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is equal to
2√10ms−1
2√3ms−1
2√2ms−1
2ms−1
The correct Answer is:C
To solve the problem of finding the magnitude of the velocity of the points at the extremities of the horizontal diameter of a wheel rolling on the ground with a speed of 2m/s, we can follow these steps:
Step 1: Understand the Motion of the Wheel
When a wheel rolls without slipping, every point on the wheel has a velocity that can be broken down into two components:
1. The translational velocity of the center of mass of the wheel.
2. The rotational velocity due to the wheel's rotation about its center.
Step 2: Identify the Components of Velocity
- The translational velocity v of the wheel's center is given as 2m/s.
- The angular velocity ω can be related to the translational velocity by the equation:
v=rω
where r is the radius of the wheel.
Step 3: Calculate the Velocity at the Extremities
For a point at the top of the wheel:
- The velocity due to translation is 2m/s (in the direction of motion).
- The velocity due to rotation (upward) is also rω=v=2m/s.
Thus, the total velocity at the top of the wheel is:
vtop=v+rω=2+2=4m/s
For a point at the bottom of the wheel:
- The velocity due to translation is 2m/s (in the direction of motion).
- The velocity due to rotation (downward) is rω=v=2m/s but in the opposite direction.
Thus, the total velocity at the bottom of the wheel is:
vbottom=v−rω=2−2=0m/s
Step 4: Conclusion
The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is:
- Top point: 4m/s
- Bottom point: 0m/s
Thus, the magnitude of the velocity of the points at the extremities of the horizontal diameter is 4m/s at the top and 0m/s at the bottom.
Final Answer
The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is 4m/s at the top and 0m/s at the bottom.
---
When a wheel rolls without slipping, every point on the wheel has a velocity that can be broken down into two components:
1. The translational velocity of the center of mass of the wheel.
2. The rotational velocity due to the wheel's rotation about its center.
- The translational velocity v of the wheel's center is given as 2m/s.
- The angular velocity ω can be related to the translational velocity by the equation:
v=rω
where r is the radius of the wheel.
For a point at the top of the wheel:
- The velocity due to translation is 2m/s (in the direction of motion).
- The velocity due to rotation (upward) is also rω=v=2m/s.
vtop=v+rω=2+2=4m/s
- The velocity due to translation is 2m/s (in the direction of motion).
- The velocity due to rotation (downward) is rω=v=2m/s but in the opposite direction.
vbottom=v−rω=2−2=0m/s
The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is:
- Top point: 4m/s
- Bottom point: 0m/s
The magnitude of the velocity of the points at the extremities of the horizontal diameter of the wheel is 4m/s at the top and 0m/s at the bottom.
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - PAST YEARS QUESTIONS70videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - ASSERTION AND REASON25videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)44videos
ROTATIONAL MOTION
- BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON18videos
NEWTON'S LAWS OF MOTION
- BOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason15videos
SIMPLE HARMONIC MOTION
Similar Questions
A wheel rolls purely on ground. Find a point on the periphery of a body which has a velocity equal to the velocity of the centre of mass of the body.
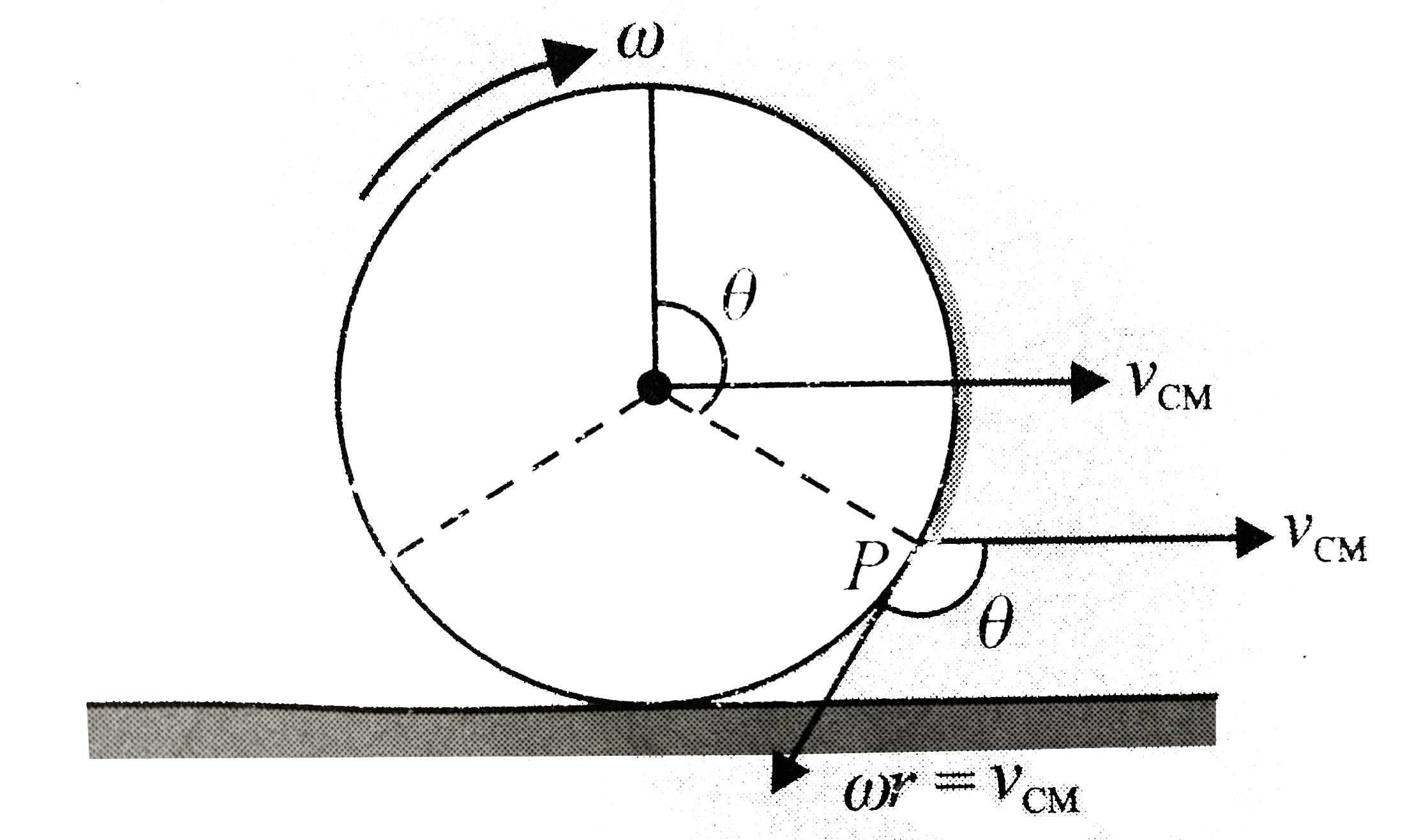 View Solution
View SolutionA wheel is rolling uniformly along a level road (see figure). The speed of transitional motion of the wheel axis is V. What are the speeds of the points A and B on the wheel rim relative to the road at the instant shown in the figure?
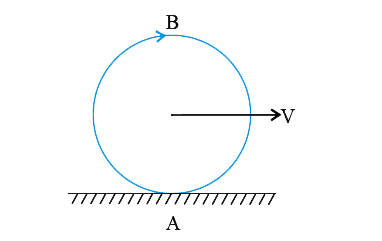 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wheel of radius R rolls on the ground with a uniform velocity v. The velocity of topmost point relative to the bottommost point is
AvB2vCv/2Dzero - Question 2 - Select One
A wheel of radius R rolls on the ground with a unifrom velocity v. The velocity of topmost point releative to bottom must point is
AzeroB2υCυDυ/2 - Question 3 - Select One
A wheel of radius 2 m rolls on the ground with uniform velocity 4ms−1. . The relative acceleration of the topmost point of the wheel with respect to the bottom - most point of the wheel is
A8ms−2B16ms−2C4ms−2D32ms−2
A sphere of radius R is rolling on a rough horizontal surface. The magnitude of velocity of A with respect to ground will be
 View Solution
View SolutionA wheel is rolling uniformly along a level road without slipping . Velocity of the highest point on its rim about the road is V . Then magnitude of velocity of a point on its rim which is at the same level as that of the centre is
View SolutionA wheel covers a distance of 1,100 cm in one round. The radius of the wheel is:
एक पहिया एक चक्कर में 1,100 सेमी की दूरी तय करता है | इस पहिये का व्यास कितना है ?View SolutionA wheel of radius 1m rolls forward half a revolution on a horizontal ground. The magnitude of the displacement of the point of the wheel initially on contact with the ground is.
View SolutionA wheel of radius R rolls on the ground with a uniform velocity v. The relative acceleration of topmost point of the wheel with respect to the bottommost point is:
View Solution

