A sphere of radius R has a volume density of charge ρ=kr, where r is the distance from the centre of the sphere and k is constant. The magnitude of the electric field which exists at the surface of the sphere is given by (ε0 = permittivity of free space)
4πkR43ε0
kR3ε0
4πkRε0
kR24ε0
The correct Answer is:D
Volume density (ρ)=kr
Total charge (q)=∫ρdv=∫R0kr4πr2dr
q=4k[r44]R0=4kR44=kR4
According to Gaussian law
∮→E.→ds=qinε0⇒E×4πR2=kR4ε0⇒E=kR24ε0
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Capacitance)59videos
ELECTROSTATICS
- BOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Grouping of Capacitors)58videos
ELECTROSTATICS
- BOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Dipole)21videos
ELECTROSTATICS
- BOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason26videos
ELECTRONICS
- BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON18videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
A solid insulating sphere of radius R has a nonuniform charge density that varies with r according to the expression ρ=Ar2, where A is a constant and rltR is measured from the centre of the sphere. Show that (a) the magnitude of the electric field outside (rgtR) the sphere is E=AR5/5ε0r2 and (b) the magnitude of the electric field inside (rltR) the sphere is E=AR3/5ε0.
 View Solution
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View Solution
Knowledge Check
- Question 1 - Select One
A sphere of radius R has a volume density of charge ρ=kr, were r is the distance from the centre of the sphere and k is constant . The magnitude of the electric field which exists at the surface of the sphere is given by (ε0= permittivity of free space)
A4πkR43ε0BkR3ε0C4πkRε0DkR24π0 - Question 2 - Select One
A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2 - Question 3 - Select One
Surface density of charge on a sphere of radius R in terms of electric intensity E at a distance in free space is
(ε0 = permittivity of free space)Aε0E(Rr)2Bε0ERr2Cε0E(rR)2Dε0ErR2
Charge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 View Solution
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
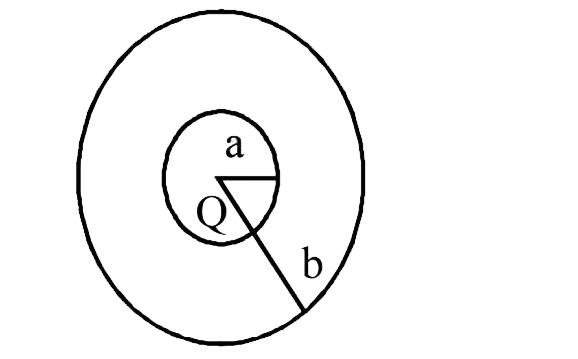 View Solution
View SolutionA Gausian sphere of radius r intercepts a line with a uniform charge density +1 as shown. The line is at a distance root 3'r/2 from the centre of the sphere. What is the electric flux associated with the Gaussian sphere?
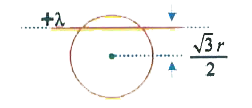 View Solution
View SolutionIf σ is the surface charge density off a charge for a charged sphere of radius R. kept in a medium of dielectric constant K, then the electric intensity at a distance r from its centre where rgtR, is (ε0=permittivity of free space)
View SolutionA system consists of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr , where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
View Solution

