A capacitor of capacity $C_{1}$ is charged to the potential of $V_{0}$ . On disconnecting with the battery, it is connected with a capacitor of capacity $C_{2}$ as shown in the adjoining figure. The ratio of energies before and after the connection of switch S will be

A

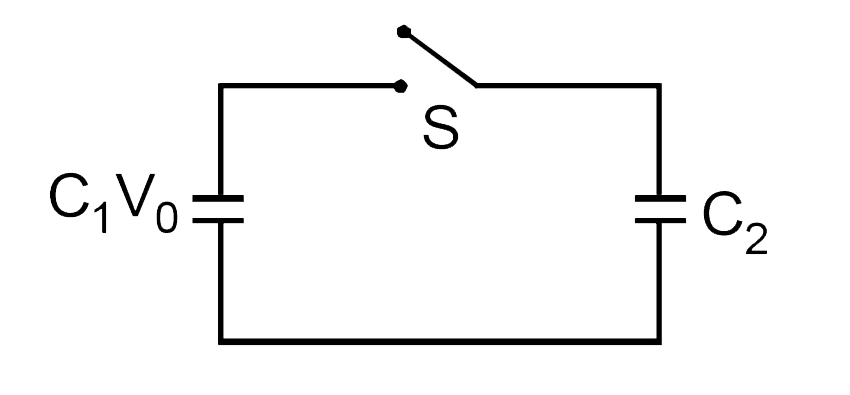
$(C_{1} + C_{2}) / C_{1}$

B

$C_{1} / (C_{1} + C_{2})$

C

$C_{1} C_{2}$

D

$C_{1} / C_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$U_{i} = \frac{1}{2} C_{1} V_{0}^{2} & Q = C V_{0}$
$U_{f} = \frac{1}{2} \frac{Q^{2}}{C_{e q}} = \frac{C_{1}^{2} V_{0}^{2}}{2 (C_{1} + C_{2})}$ [as Q = constant]
$\frac{U_{i}}{U_{f}} = \frac{C_{1} V_{0}^{2}}{C_{1}^{2} V_{0}^{2}} \times (C_{1} + C_{2}) = \frac{(C_{1} + C_{2})}{C_{1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A capacitor of capacity $C_{1}$ is charged to the potential of $V_{0}$ . On disconnecting with the battery, it is connected with a capacity $C_{2}$ as shown in the adjoining figure. The ratio of energies before and after the connection of switch $S$ will be

A $(C_{1} + C_{2}) / C_{1}$
B $C_{1} / (C_{1} + C_{2})$
C $C_{1} C_{2}$
D $C_{1} / C_{2}$
Question 2 - Select One or More
A capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then
AEnergy stored in capacitor and inductor will be equal at time $t = \frac{π}{2} \sqrt{L} C$
BPotential difference across inductor will be $\frac{V}{2}$ at time $t = \frac{π}{3} \sqrt{L} C$
CThe rate of increase of energy in magnetic field will be maximum at $\frac{π}{4} \sqrt{L} C$
DWhen the potentail difference across the capacitor $\sqrt{(\frac{3 C}{L})}$
Question 3 - Select One
A capacitor of capacity $C_{1} = 1 μ F$ is charged to a potential of 100 V. The charging battery is then removed and it is connected to another capacitor of capacity $C_{2} = 2 μ F$ . One plate of $C_{2}$ is earthed as shown in figure. The charges on $C_{1} and C_{2}$ in steady state will be

A $50 μ C, 50 μ C$
B $100 μ C, z e r o$
C $\frac{100}{3} μ C, \frac{200}{3} μ C$
Dzero,zer

ERRORLESS-ELECTROSTATICS-NCERT BASED QUESTIONS (Grouping of Capacitors)

Home
Ask Doubt
Profile