A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
mglsinθ
mgl(1+sinθ)
mgl(1+cosθ)
mgl(1−cosθ)
The correct Answer is:D
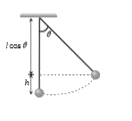
h=l−lcosθ
=l(1−cosθ)
According to law of conservation
KE=PE=mg h
⇒KE=mgl(1−cosθ).
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Spring Pendulum)
30 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Superposition of S.H.M.s and Resonance)
7 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - NCERT BASED QUESTIONS (Time Period and Frequency)
7 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - Assertion & Reason
25 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
Similar Questions
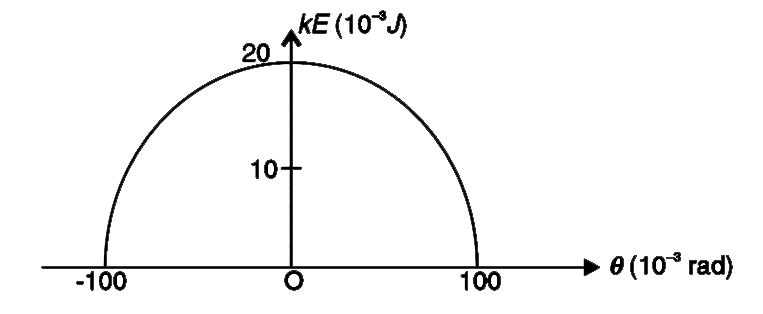
The given figure shows the variation of the kinetic energy of a simple pendulum with its angular displacement (θ) from the vertical. Mass of the pendulum bob is m = 0.2 kg. Find the time period of the pendulum. Take g=10ms−2.
View SolutionA string of length l and mass m is fixed at both ends with tension t and excited in its fundamental mode.The maximum displacement at the mid point is A Find (a) the maximum kinetic energy of the string ,9b0 the mean kinetic energy of the srting averaged over one oscillation period
hint Take sine distribution of amplitudes
View Solution
Knowledge Check
A simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
Amgl(1−cosθ)BmglcosθCmglsinθDNone of theseIf a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
A√LgB2√glsin(θ2)C√2glsinθD√2glA simple pendulum is oscillating with a maximum angular displacement of θ radian. If θ is very small, the ratio of maximum tension to the minimum tension in the string during oscillations is
A(1+θ2):(1−θ2)B(1+θ2):(1−θ22)C(1+θ2):1D(1+θ22):(1−θ2)
A simple pendulum having a bob of mass 100 g is oscillating with a maximum angular displacement of 3∘. The maximum restoring force acting on the bob is (take g=10ms−2)
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionKinetic energy of the bob of a simple pendulum is maximum
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA simple pendulum oscillates with maximum displacement θ0 The time taken, when pendulum displaces from 0 to θ02 is t1 and time taken when pendulum displaces from θ02 to θ0 is t2 then what is true ?
View Solution
