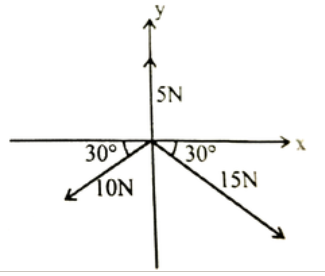
Find the magnitude of the resultant of shown forces :-
2A, 200V
1.5A, 100V
2.7A, 220V
2.2 A, 220 V
The correct Answer is:D
Since VC=VL=200V
V=√V2R+(VC−VL)2
⇒V=VR Reading of voltmeter = 220 V
Current I=VR=220100=2.2A
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - ERRORLESSCHAPTER - ALTERNATING CURRENTEXERCISE - Past Years Questions
30 Videos
- ALTERNATING CURRENTBOOK - ERRORLESSCHAPTER - ALTERNATING CURRENTEXERCISE - Assertion & Reason
13 Videos
- ALTERNATING CURRENTBOOK - ERRORLESSCHAPTER - ALTERNATING CURRENTEXERCISE - Assertion & Reason
13 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
Similar Questions
The maximum and minimum magnitudes of the resultant of two forces are 5 N and 5N respectively. Find the magnitude of resultant force when act orthogonally to each other.
View SolutionTwo forces of magnitudes P and Q are inclined at an angle (θ). The magnitude of their resultant is 3Q. When the inclination is changed to (180∘−θ), the magnitude of the resultant force becomes Q. Find the ratio of the forces.
View Solution
Knowledge Check
The greatest & the least magnitude of the resultant of two forces of constant magnitudes are P & Q respectively. If the forces act at an angle 2α, then prove that the magnitude of their resultant is given by √P2cos2α+Q2sin2α.
A√(F2cos2α+G2sin2α)B√(F2sin2α+G2cos2α)C√(F2+G2)D√(F2−G2)Two forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
Acos−1(−1718)Bcos−1(−13)Ccos−1(−23)Dcos−1(−89)Two forces with equal magnitudes F act on a body and the magnitude of the resultant force is F /3. The angle between the two forces is
Acos−1(−1718)Bcos−1(−13)Ccos−1(23)Dcos−1(89)
The sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90∘ with the force of smaller magnitude, What are the magnitudes of forces?
View SolutionIf two forces are acting at a point such that the magnitude of each force is 2 N and the magnitude of their resultant is also 2 N, then the angle between the two forces is
View SolutionTwo parallel forces F1 and F2 acting in the same direction are applied to a rigid body.
Porve that
(a) the magnitude of the resultant force is equal to the sum of magnitudes of the forces being added,
(b) the resultant force is parallel to the forces being added and acts in the same direction,
(c ) the resultant force passes through the centre of the parallel forces, i.e. through the point which divides the distance between the points of application of both forces into sections inversely proportional to the magnitude of the forces.
View SolutionTwo forces, with equal magnitude F, act on a body and the magnitude of the resultant force is F3. The angle between the two forces is:
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at 90∘ with the force of smaller magnitude, then their magnitudes are
View Solution
