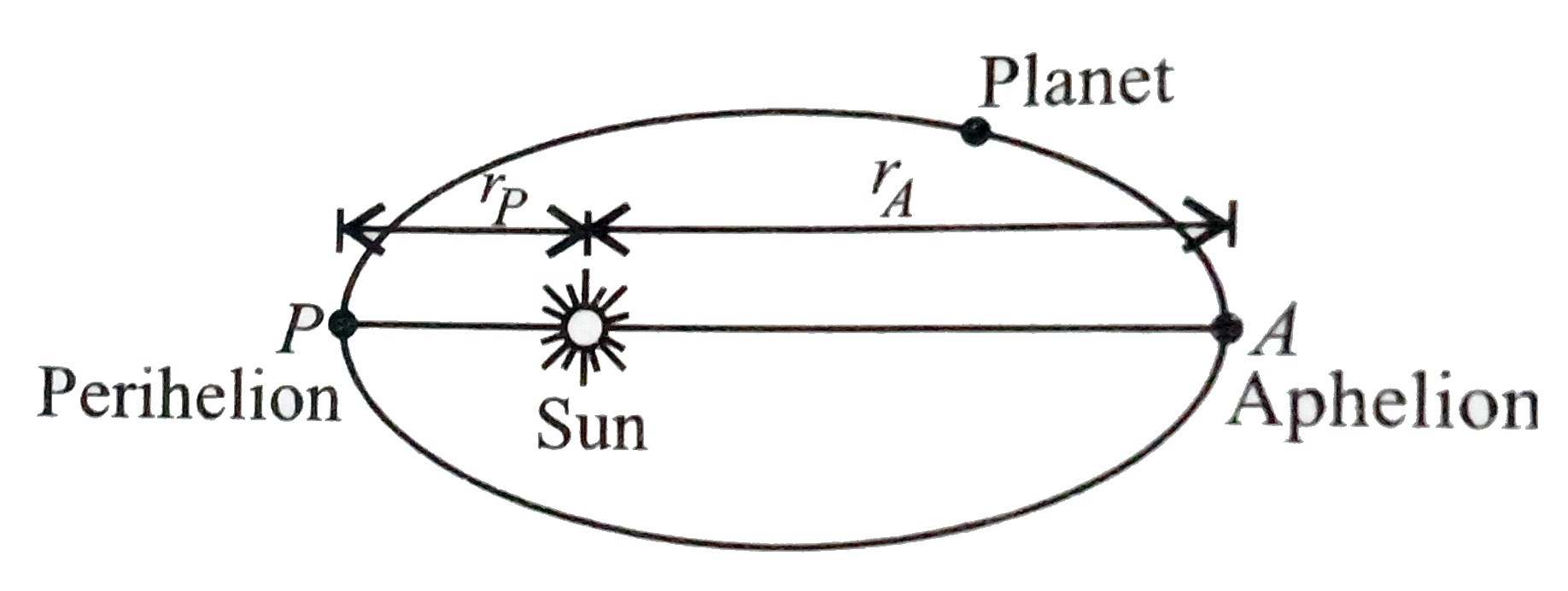
A planet orbits in an elliptical path of eccentricity e around a massive star considered fixed at one of the foci. The point in space where it is closest to the star is denoted by P and the point where it is farthest is denoted by A. Let and be the respective speeds at P and A. Then–

The correct Answer is:A
Angular momentum conservation about S
Topper's Solved these Questions
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS (Kepler’s Laws of Planetary Motion)
27 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - Past Years Questions
36 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS (Gravitation Potential, Energy and Escape Velocity)
38 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - ASSERTION AND REASON
16 Videos
Similar Questions
A satellite is in an elliptical orbit around a planet P. It is observed that the velocity of the satellite when it is farthest from the planet is 6 times less than that when it is closest to the planet . The ratio of distances between the statellite and the planet at closest and farthest points is :
View SolutionThe radius of a planet is twice that of the earth but its average density is the same. If the escape speed at the planet and at the earth are vp and ve, respectively, then prove that vp=2ve
View Solution
Knowledge Check
A planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1 At another point Q, when it is farthest from the sun at a distance d2 its speed will be
Ad21d22.v1Bd2d1.v1Cd22d21.v1Dd1v1d2A planet moves around the sun. at a given point P, it is closest from the sun at a distance d1, and has a speed V1. At another point Q, when it is farthest from the sun at a distance d2, its speed will be
Ad21V1d2Bd2V1d1Cd1V1d2Dd22V1d21A planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1. At another point Q, when it is farther from the sun at a distance d2, its speed will be
Ad21d22v1Bd2d1v1Cd22d21v1Dd1v1d2
A planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
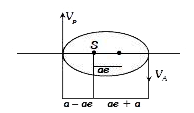
View SolutionA planet orbits the sun in an elliptical path as shown in the figure. Let vp and vA be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
View SolutionA disc is rolling without slipping on a horizontal surface with C, as its centre and Q and P the two points equidistant from C. Let vP,vQandvC be the magnitudes of velocities of point P,Q and C respectively, then

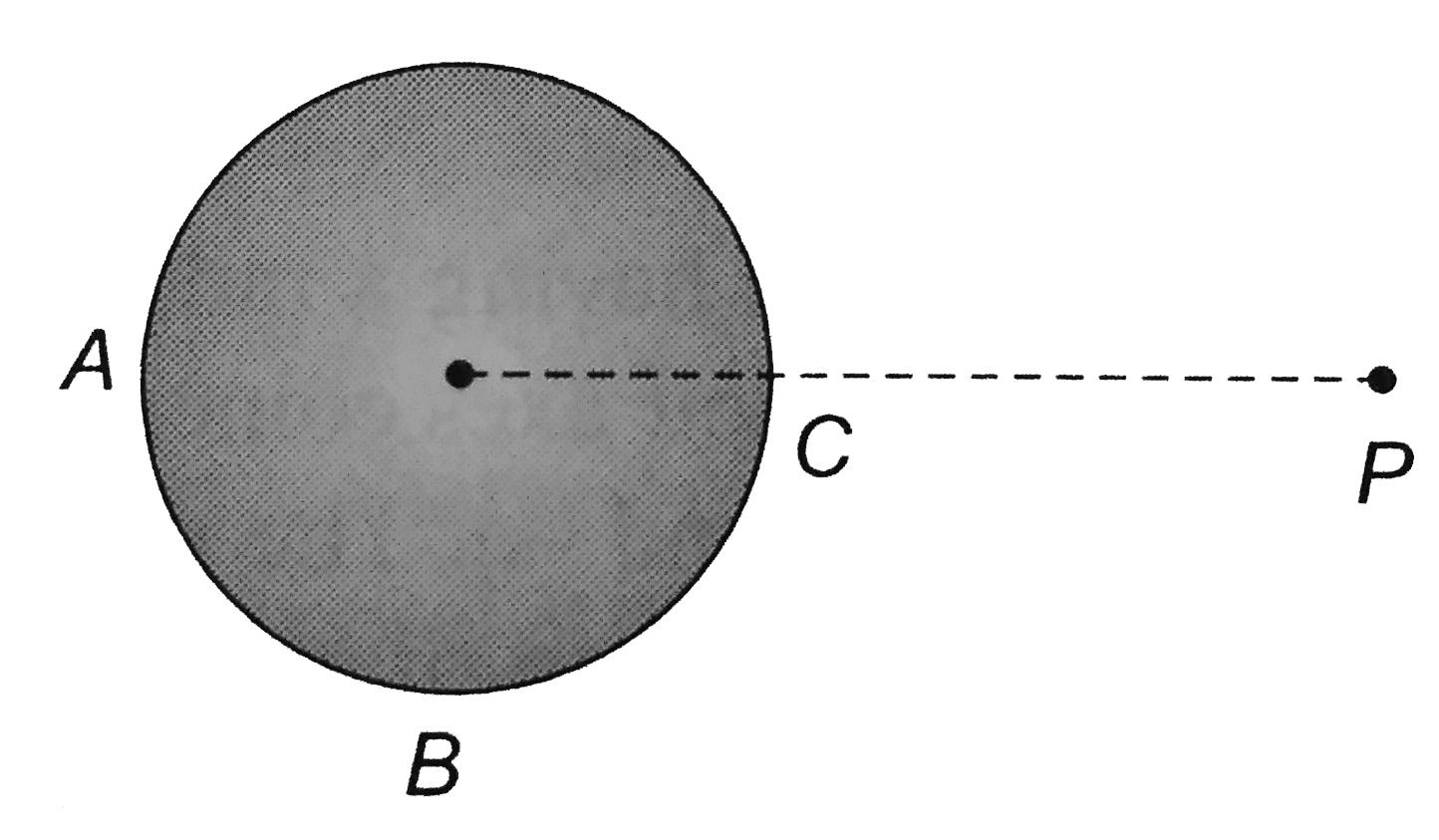
View SolutionA hollow conducting sphere is placed in an electric field produced by a point charge placed at P as shown in figure.
Let VA,VB,VC be the potentials at points A,BandC respectively. Then
View SolutionA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
View Solution
