Two resistances R1 and another R2 of the same material but twice the length and half the thickness are connected in series with a standard battery E of internal resistance r. The balancing point is-
18l
14l
8l
16 l
The correct Answer is:C
To solve the problem, we need to find the balancing point for two resistances R1 and R2 connected in series with a battery of EMF E and internal resistance r. The resistances are made of the same material, but R2 is twice the length and half the thickness of R1.
1. Determine the Resistance of Each Wire:
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
2. Calculate the Cross-Sectional Area:
The cross-sectional area A of a wire with radius r is:
A=πr2
If the thickness is halved, the new radius r2 becomes r12, hence:
A2=π(r12)2=πr214=A14
3. Express the Resistances:
For R1:
R1=ρL1A1
For R2 (twice the length and half the thickness):
R2=ρ(2L1)A14=8ρL1A1=8R1
4. Total Resistance in Series:
The total resistance Rt in the circuit is:
Rt=R1+R2+r=R1+8R1+r=9R1+r
5. Potential Gradient:
The potential gradient ϕ is given by:
ϕ=VL
where V is the potential difference across the resistances.
6. Balancing Point:
We can set up the equations for the potential drops across R1 and R2 when the galvanometer shows zero deflection (balancing point):
ϕL1=ER19R1+r
ϕL2=E(8R1)9R1+r
7. Setting Up the Ratio:
From the balancing point condition:
ϕL1ϕL2=L1L2=R18R1=18
Thus, L2=8L1.
8. Conclusion:
The balancing point occurs at a distance L1 from one end, which corresponds to 18 of the total length L of the wire.
Final Answer:
The balancing point is at 18L.
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
The cross-sectional area A of a wire with radius r is:
A=πr2
If the thickness is halved, the new radius r2 becomes r12, hence:
A2=π(r12)2=πr214=A14
For R1:
R1=ρL1A1
For R2 (twice the length and half the thickness):
R2=ρ(2L1)A14=8ρL1A1=8R1
The total resistance Rt in the circuit is:
Rt=R1+R2+r=R1+8R1+r=9R1+r
The potential gradient ϕ is given by:
ϕ=VL
where V is the potential difference across the resistances.
We can set up the equations for the potential drops across R1 and R2 when the galvanometer shows zero deflection (balancing point):
ϕL1=ER19R1+r
ϕL2=E(8R1)9R1+r
From the balancing point condition:
ϕL1ϕL2=L1L2=R18R1=18
Thus, L2=8L1.
The balancing point occurs at a distance L1 from one end, which corresponds to 18 of the total length L of the wire.
The balancing point is at 18L.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (HEATING EFFECT OF CURRENT)
67 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - PAST YEARS QUESTIONS
76 Videos
- CURRENT ELECTRICITYBOOK - ERRORLESSCHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT BASED QUESTIONS (KIRCHHOFF.S LAW, CELLS)
53 Videos
- ATOMIC AND NUCLEAR PHYSICSBOOK - ERRORLESSCHAPTER - ATOMIC AND NUCLEAR PHYSICSEXERCISE - Assertion and Reason
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ERRORLESSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON
20 Videos
Similar Questions
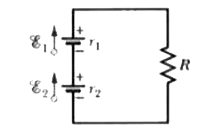
In Fig. 27-51. battery 1 has emf ε1=12.0V and internal resistance r1=0.025Ω and battery 2 has emf2=12.0V and internal resistance r2=0.012Ω. The batteries are connected in series with an external resistance R. (a) What R value makes the terminal-to-terminal potential difference of one of the batteries zero? (b) Which battery is that?
View SolutionA voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find R1 and R2 in terms of R.
View Solution
Knowledge Check
A cell of e.m.f E is connected to a resistance R1 for time i and the amount of heat generated in it is H. If the resistance R1 is replaced by another resistance R2 and is connected to the cell for the same time i, the amount of heat generated in R2 is 4H. Then the internal resistance of the cell is
A2R1+R22B√R1R22√R2−√R1√R2−2√R1C√R1R2√R2−2√R12√R2−√R1D√R1R2√R2−2√R12√R2+√R1AB is a potentiometer wire of length 100cm and its resistance is 10ohm. It is connected in series with a resistance R=40 ohm and a battery of e.m.f. wV and negigible internal resistance. If a source of unknown e.m.f. E is balanced by 40cm length of the potentiometer wire, the value of E is:
 A0.8VB1.6VC0.08VD0.16V
A0.8VB1.6VC0.08VD0.16VA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A(1n)B1(n+1)Cn(n+1)D(n+1)n
A voltmeter of resistance RV and an ammeter of resistance RA are connected in series across a battery of emf E and of negligible internal resistance . When a resistance R is connected in parallel to volmeter , reading of ammeter increases to three times while that of volmeter reduces to one - third. Calculate RAandRV in terms of R.
View SolutionTwo square metal plates A and B are of same thickness and material. The side of B is twice that of A. These are connected in series, as shown in Fi. 4.3. Find the ratio RA/RB of the resistance of the two plates.
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionN batteries each of emf E and internal resistance r are first connected in series and then in parallel to an external resistance R. if current through R is same in both cases then.
View SolutionTwo batteries one of the emf3V, internal resistance In and the other of emf l SV, internal resistance 2Ω are connected in series with a resistanceR as shown. If the potential difference between points a and b is zero, the resistance R is :
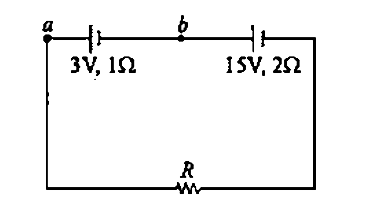
View Solution
