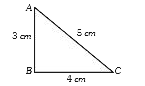
A 12 cm wire is given a shape of a right angled triangle ABC having sides 3 cm, 4 cm and 5 cm, as shown in the figure. The resistance between two ends (AB, BC, CA) of the respective sides are measured one by one by a multi-meter. The resistances will be in the ratio-

A

$9 : 16 : 25$

B

$27 : 32 : 35$

C

$21 : 24 : 25$

D

$3 : 4 : 5$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$R_{A B} = \frac{9 \times 3}{9 + 3} = \frac{27}{12}$
$R_{B C} = \frac{8 \times 4}{8 + 4} = \frac{32}{12}$
$R_{A C} = \frac{7 \times 5}{7 + 5} = \frac{35}{12}$
as $R \propto l$
$R_{A B} : R_{B C} : R_{A C} = 27 : 32 : 35$

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
A1 cm
B1.25 cm
C1.5 cm
D2 cm
Question 2 - Select One
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :

A1 cm
B1.25 cm
C1.5 cm
Dnone of these
Question 3 - Select One
A right angled $△$ ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. The volume of the solid so obtained is
A200 $π c m^{3}$
B211 $π c m^{3}$
C100 $π c m^{3}$
D101 $π c m^{3}$

ERRORLESS-CURRENT ELECTRICITY-PAST YEARS QUESTIONS

Home
Ask Doubt
Profile