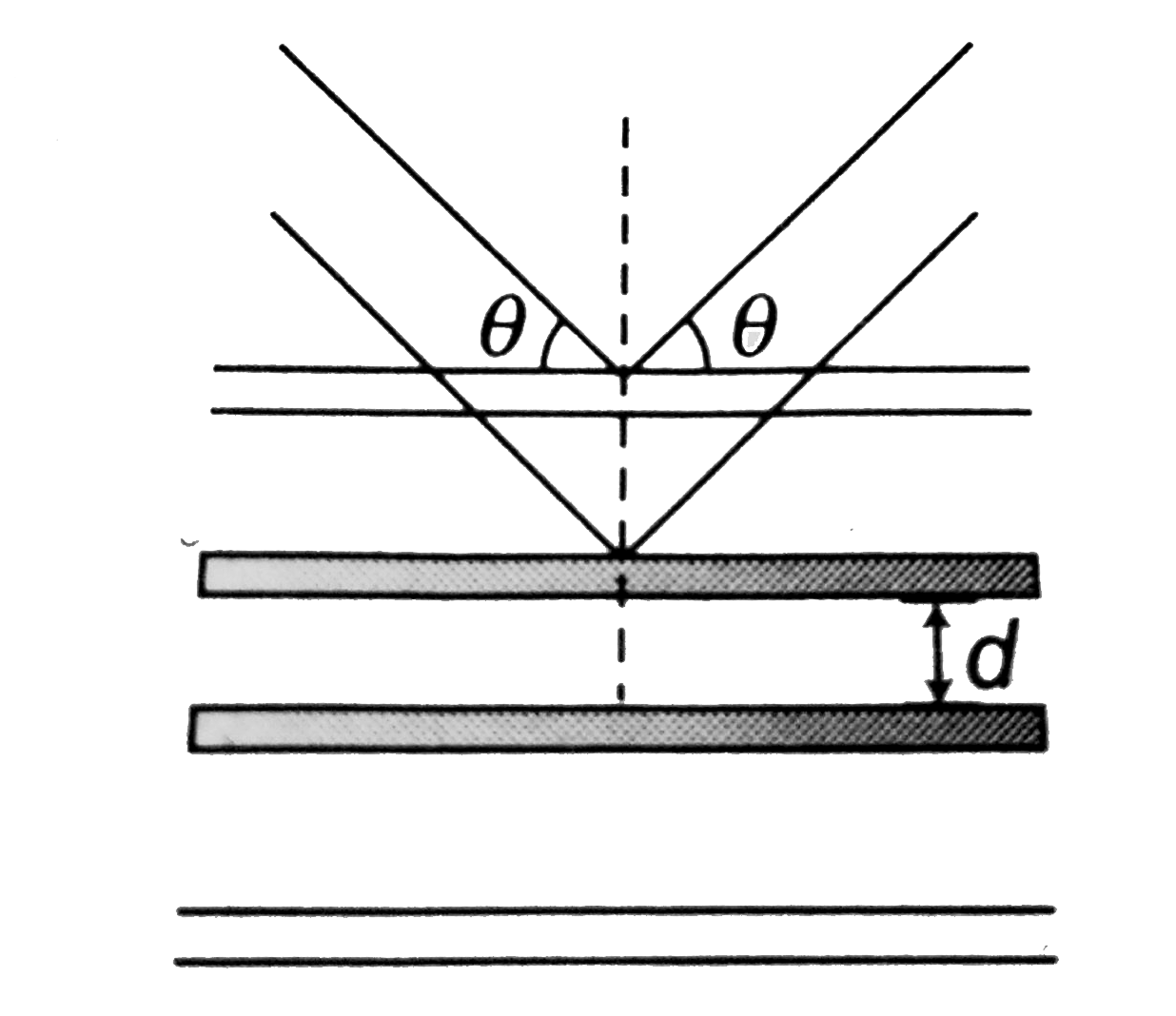
A beam with wavelength λ falls on a stack of partially reflecting planes with separation d. The angle θ that the beam should make with planes so that the beams reflected from successive planes may interfere constructively is (where n=1, 2, ...)
sin(nλd)
sin−1(nλd)
sin−1(nλ2d)
cos−1(nλ2d)
The correct Answer is:C
Path difference = 2dsinθ For constructive interference 2dsinθ=nλ
θ=sin−1(nλ2d)
Topper's Solved these Questions
- WAVE OPTICS AND ELECTROMAGNETIC THEORYBOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - NCERT BASED QUESTIONS (Diffraction of Light)
20 Videos
- WAVE OPTICS AND ELECTROMAGNETIC THEORYBOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - NCERT BASED QUESTIONS (Polarization of Light)
17 Videos
- WAVE OPTICS AND ELECTROMAGNETIC THEORYBOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - ASSERTION & REASON
27 Videos
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - Assertion & Reason
30 Videos
Similar Questions
Demostrate that a light beam reflected from three mutually perpendicular plane mirrors in succession reverses its direction.
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly S4 T z reflects the light ?
View Solution
Knowledge Check
A beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
A916×λB3λ/4Cλ×43DλWhen a plane mirror is rotated through an angle θ then the reflected ray turns through the angle 2θ then the size of the image
AIs doubledBIs halvedCRemins the sameDBecomes infiniteTwo identical beam A and B of plane coherent waves of the sasme intensity and wavelength λ fall on a plane screen. The direction of the beam propagations make angles θ1 and θ2 with the normal to the screen and lie in the same plane as shown in the figure. Find the distance β between adject interfrence fringes on the screen.
 Aλsinθ−sinθ2Bλsinθ1+sinθ2Cλ(sinθ1−sinθ2)sinθ1+sinθ2Dλ(sinθ1+sinθ2)sinθ1−sinθ2
Aλsinθ−sinθ2Bλsinθ1+sinθ2Cλ(sinθ1−sinθ2)sinθ1+sinθ2Dλ(sinθ1+sinθ2)sinθ1−sinθ2
Unpolarized light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to eachother ?
View SolutionA beam of parallel rays of width b propagates in glass at an angleθto its plane face .The beam width after it goes over to air through this faceis…….if the refractive index of glass is μ.v
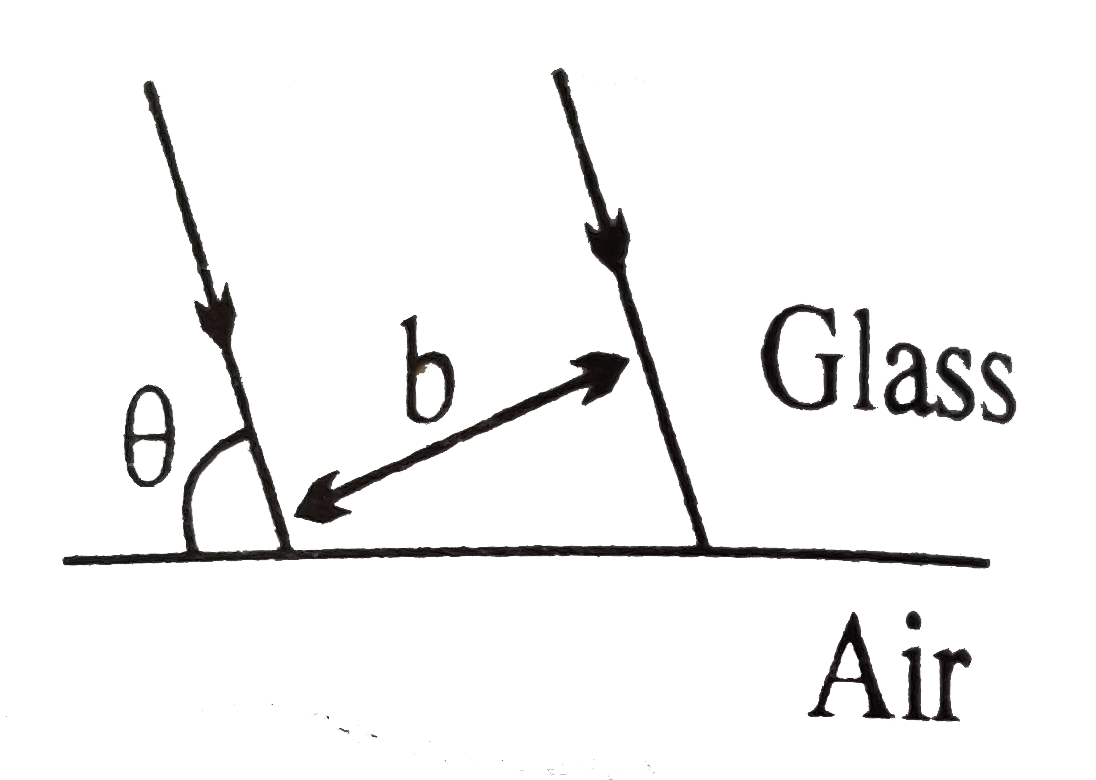
View SolutionLight of wavelength 5000Å falls on a plane reflecting surface. What are the wavelength and frequency of reflected light ? For what angle of incidence is the reflected ray normal to the incident ray ?
View SolutionA plane mirror rotating at an angular velocity of 3 radian/s reflects a light beam. The angular velocity of the reflected beam is -
View SolutionA beam of monochromatic light of wavelength λ falls normally on a diffraction grating of line spacing d. If θ is the angle between the second-order diffracted beam and the direction of the incident light, what is the value of sinθ ?
View Solution
