A and B are two parallel sided transparent slabs of refractive indices n1 andn2 respectively. A ray is incident at an angle θ on the surface of separation of A and B and after refraction from B into air grazes the surface of B. Then
sinθ=1n2
sinθ=1n1
sinθ=n2n1
sinθ=n1n2
The correct Answer is:B
To solve the problem, we need to analyze the refraction of light as it passes through two transparent slabs (A and B) with different refractive indices and then exits into air. We will apply Snell's law to find the relationship between the angles of incidence and refraction.
1. Identify the Given Information:
- Refractive index of slab A: n1
- Refractive index of slab B: n2
- Angle of incidence on the surface of separation: θ
2. Apply Snell's Law at the Interface of Slab A and Slab B:
- When the ray of light strikes the surface separating slabs A and B, we can use Snell's law:
n1sin(θ)=n2sin(θ2)
- Here, θ2 is the angle of refraction in slab B.
3. Determine the Condition for Grazing Refraction:
- The problem states that the ray grazes the surface of slab B when it exits into air. This means that the angle of refraction at the interface between slab B and air is 90∘.
- According to Snell's law at the interface of slab B and air:
n2sin(θ2)=nairsin(90∘)
- Since sin(90∘)=1 and the refractive index of air nair is approximately 1, we can write:
n2sin(θ2)=1
- Therefore, we can express sin(θ2) as:
sin(θ2)=1n2
4. Substitute sin(θ2) Back into Snell's Law:
- From the first application of Snell's law, we have:
n1sin(θ)=n2sin(θ2)
- Substituting sin(θ2):
n1sin(θ)=n2(1n2)
- This simplifies to:
n1sin(θ)=1
5. Final Relation:
- Rearranging gives us:
sin(θ)=1n1
- This equation describes the relationship between the angle of incidence θ and the refractive index n1 of slab A.
Summary:
The final relation derived from the conditions given in the problem is:
sin(θ)=1n1
- Refractive index of slab A: n1
- Refractive index of slab B: n2
- Angle of incidence on the surface of separation: θ
- When the ray of light strikes the surface separating slabs A and B, we can use Snell's law:
n1sin(θ)=n2sin(θ2)
- Here, θ2 is the angle of refraction in slab B.
- The problem states that the ray grazes the surface of slab B when it exits into air. This means that the angle of refraction at the interface between slab B and air is 90∘.
- According to Snell's law at the interface of slab B and air:
n2sin(θ2)=nairsin(90∘)
- Since sin(90∘)=1 and the refractive index of air nair is approximately 1, we can write:
n2sin(θ2)=1
- Therefore, we can express sin(θ2) as:
sin(θ2)=1n2
- From the first application of Snell's law, we have:
n1sin(θ)=n2sin(θ2)
- Substituting sin(θ2):
n1sin(θ)=n2(1n2)
- This simplifies to:
n1sin(θ)=1
- Rearranging gives us:
sin(θ)=1n1
- This equation describes the relationship between the angle of incidence θ and the refractive index n1 of slab A.
The final relation derived from the conditions given in the problem is:
sin(θ)=1n1
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( Total internal reflection )26videos
RAY OPTICS
- BOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( Refraction at Curved surface )61videos
RAY OPTICS
- BOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( SPHERICAL MIRROR )23videos
RAY OPTICS
- BOOK - ERRORLESSCHAPTER - MAGNETISMEXERCISE - Assertion and Reason22videos
MAGNETISM
- BOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - ASSERTION & REASON27videos
WAVE OPTICS AND ELECTROMAGNETIC THEORY
Similar Questions
A,B, and C are the parallel sided transparent media of refractive indices n1,n2 and n3 respectively. They are arranged as shown in the figure. A ray is incident at an angle i on the surface of separation of A and B which is as shown in the figure. After the refraction into the medium B the ray grazes the surfaces of separation of the media B and C. then sini equal to
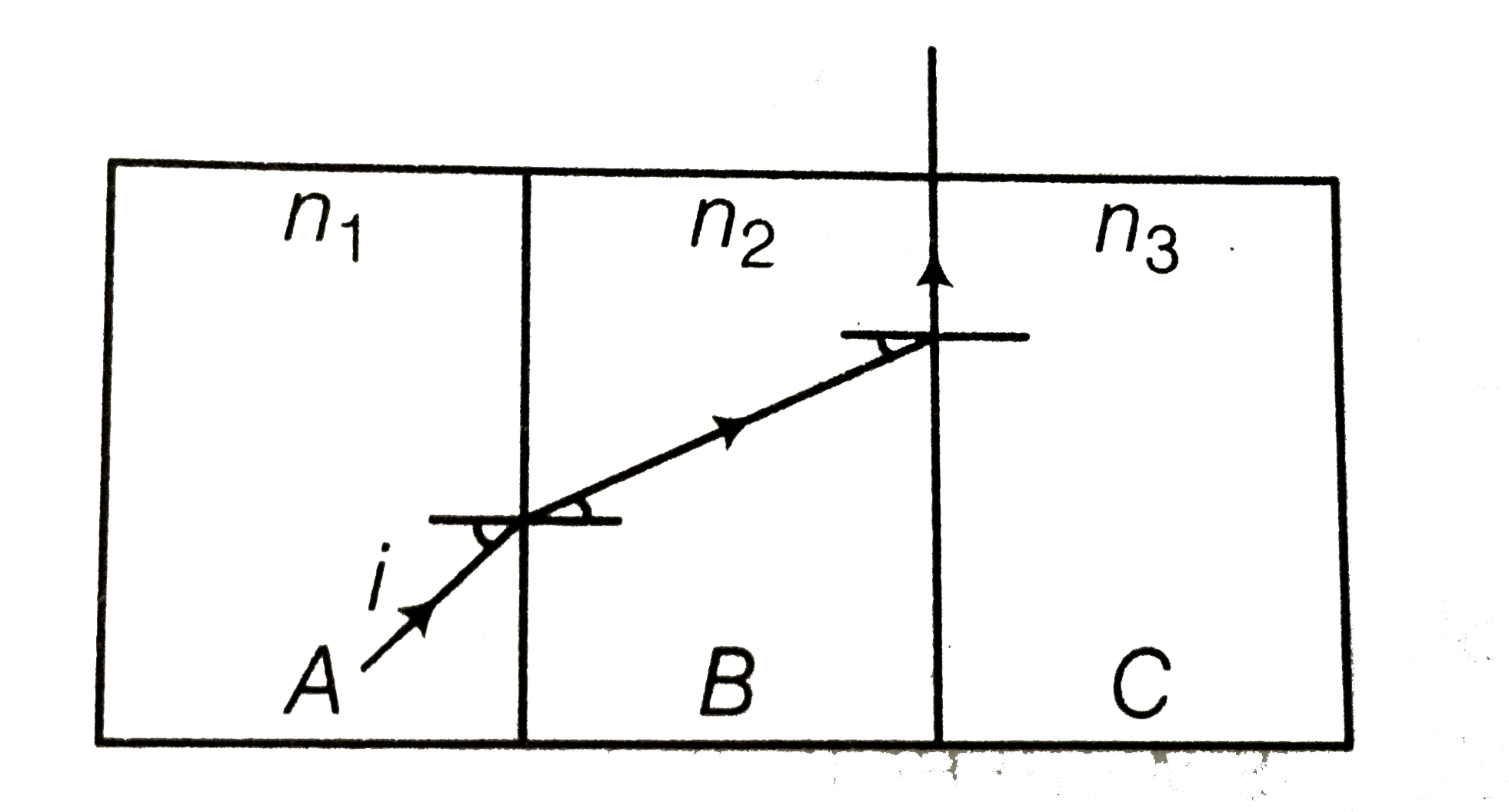 View Solution
View SolutionA equilateral glass prism has a refractive index √(2) . A light ray is incident at 45^∘ on one face.Total deviation of ray after refraction from second surface is n times15^(0) where 'n' is
View Solution
Knowledge Check
- Question 1 - Select One
AN unpolarised beam of light is incident at the polarising angle on the surface of a transparent medium of refractive index 1.6. The angle of refraction in the medium is
A58∘B29∘C32∘D42∘ - Question 2 - Select One
A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
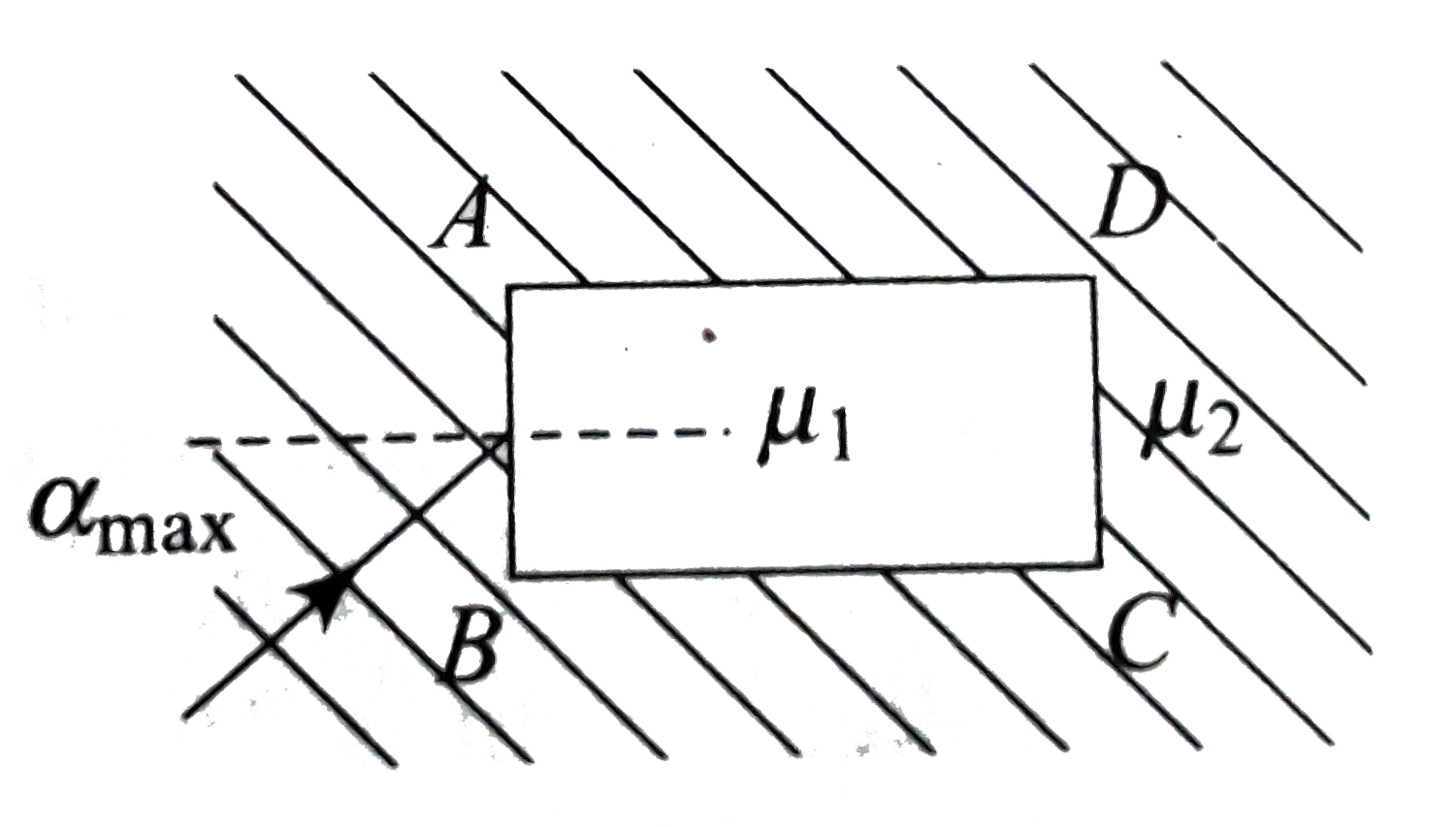 Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1) - Question 3 - Select One
A rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
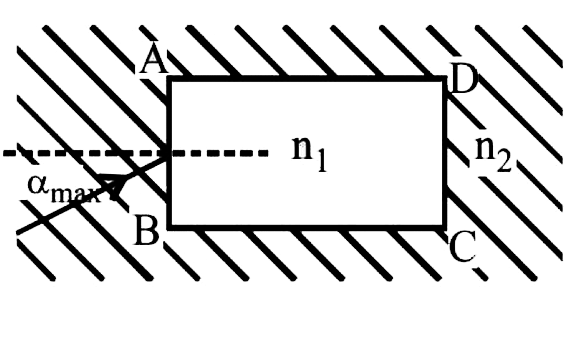 Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
A ray of light is incident on the surface of a glass plate of index of refraction 1.55 at the polarizing angle. Calculate the angle of refraction.
View SolutionA ray is incident on a slab of refractive index 5/4 at an angle /θ as shown. Find maximum angle /θ so that TIR occur at surface AD.
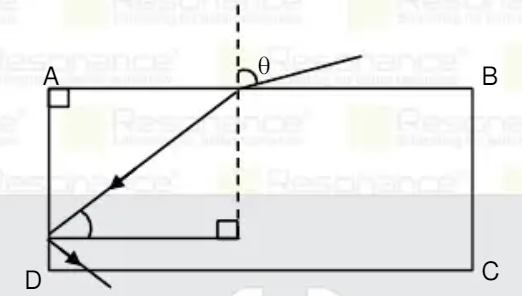 View Solution
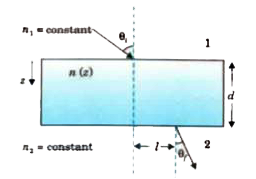
View SolutionA transparent slab of thickness d has a refractive index n(z) that increases with z. Here z is the vertical distance inside the slab, measured from the top. The slab is placed between two media with uniform refractive indices n1andn2(>n1), as shown in the figure. A ray of light is incident with angle θi, from medium 1 and emerges in medium 2 with refraction and θf, with a lateral displacement l.
Which of the following statement(s) is (are) true ?View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle betweent the reflected and refracted rays is
View SolutionA ray of light strikes a transparent rectangular slab of refractive index √2 at an angle of incidence of 45∘. The angle between the reflected and refracted rays is
View Solution
