Two similar thin equi-convex lenses, of focal f each, are kept coaxially in contact with each other such that the focal length of the combination is F1, When the space between the two lens is filled with glycerin (which has the same refractive index (μ=1.5) as that of glass) then the equivalent focal length is F2, The ratio F1:F2 will be
A
3:4
B
2:1
C
1:2
D
2:3
Video Solution
Text Solution
The correct Answer is:C
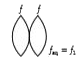
1f1=1f+1f=2f
f1=f2=R2
1f=(1.5−1) 2 /R
=12×2R=1R
1f2=1R−1R+1R=1R
f2= R
with glycerin : focal length of concave lens is formed
1f.=(m−1)(−1R−1R)=12(−2R)=−1R
f1f2=R2R=12
|
Topper's Solved these Questions
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - Assertion & Reason
30 Videos
- RAY OPTICSBOOK - ERRORLESSCHAPTER - RAY OPTICSEXERCISE - NCERT BASED QUESTIONS ( Microscope and Telescope)
34 Videos
- MAGNETISMBOOK - ERRORLESSCHAPTER - MAGNETISMEXERCISE - Assertion and Reason
22 Videos
- WAVE OPTICS AND ELECTROMAGNETIC THEORYBOOK - ERRORLESSCHAPTER - WAVE OPTICS AND ELECTROMAGNETIC THEORYEXERCISE - ASSERTION & REASON
27 Videos
Similar Questions
Knowledge Check
Two similar thin equi-convex lenses, of focal f each, are kept coaxially in contact with each other such that the focal length of the combination is F1, When the space between the two lens is filled with glycerin (which has the same refractive index (μ=1.5) as that of glass) then the equivlent focal length is F2, The ratio F1:F2 will be
A2:1B1:2C2:3D3:4Two thin lenses of focal lengths f1 and f2 are placed in contact with each other. The focal length of the combination is :
Af1+f22B√f1f2Cf1f2f1+f2Df1f2f1−f2Two thin lenses of focal lengths f1 and f2 are placed in contact with each other. The focal length of the combination is :
Af1+f22B√f1f2Cf1f2f1+f2Df1f2f1−f2
A concave lens of focal length 12 cm and a convex lens of focal length 20 cm are kept in contact with each other .
Find the focal length of the combination .
View SolutionTwo thin lenses of power +3Dand−1D are held in contact with each other. Focal length of the combination is :
View SolutionA convex lens of focal length f1 is kept in contact with a concave lens of focal length f2. Find the focal length of the combination.
View SolutionTwo thin converging lenses of focal length 15 cm and 30 cm are held in contact with each other. The focal length of the combination is
View SolutionTwo convex lenses with power 2 dioptre are kept in contact
with each other. The focal length of the combined lens
system is
View Solution
