Near the surface of earth, an electric field points radially downward and has a magnitude of approximately 100N/C.
What charge (magnitude and sign) would have to be placed on a penny that has a mass of 3.11g to cause it to rise into the air with an upward acceleration of 1.990 ms2 ? (Express your answer to three significant figures)
To solve the problem, we need to determine the charge that must be placed on a penny to achieve a specific upward acceleration in the presence of a downward electric field.
1. Identify the Forces Acting on the Penny:
- The gravitational force acting on the penny (downward) is given by Fg=mg.
- The electric force acting on the penny (upward) is given by Fe=qE, where q is the charge on the penny and E is the electric field strength.
2. Set Up the Equation of Motion:
- According to Newton's second law, the net force acting on the penny is equal to the mass of the penny multiplied by its acceleration:
Fnet=ma
- The net force can also be expressed as the difference between the electric force and the gravitational force:
Fe−Fg=ma
- Substituting the expressions for Fe and Fg:
qE−mg=ma
3. Rearranging the Equation:
- Rearranging the equation gives us:
qE=mg+ma
- Factoring out m on the right side:
qE=m(g+a)
4. Solving for Charge q:
- Now, we can solve for the charge q:
q=m(g+a)E
5. Substituting Known Values:
- Given:
- Mass of the penny, m=3.11g=3.11×10−3kg
- Gravitational acceleration, g=9.81m/s2
- Upward acceleration, a=1.990m/s2
- Electric field strength, E=100N/C
- Substituting these values into the equation:
q=(3.11×10−3kg)×(9.81m/s2+1.990m/s2)100N/C
6. Calculating the Charge:
- First, calculate g+a:
g+a=9.81+1.990=11.800m/s2
- Now substitute this back into the equation for q:
q=(3.11×10−3)×(11.800)100
q=0.036758100=3.6758×10−4C
7. Expressing the Charge in Microcoulombs:
- Convert to microcoulombs:
q=367.58μC≈368μC
- Since the charge must be negative to counteract the downward electric field:
q≈−368μC
Final Answer:
The charge that must be placed on the penny is approximately −368μC.
- The gravitational force acting on the penny (downward) is given by Fg=mg.
- The electric force acting on the penny (upward) is given by Fe=qE, where q is the charge on the penny and E is the electric field strength.
- According to Newton's second law, the net force acting on the penny is equal to the mass of the penny multiplied by its acceleration:
Fnet=ma
- The net force can also be expressed as the difference between the electric force and the gravitational force:
Fe−Fg=ma
- Substituting the expressions for Fe and Fg:
qE−mg=ma
- Rearranging the equation gives us:
qE=mg+ma
- Factoring out m on the right side:
qE=m(g+a)
- Now, we can solve for the charge q:
q=m(g+a)E
- Given:
- Mass of the penny, m=3.11g=3.11×10−3kg
- Gravitational acceleration, g=9.81m/s2
- Upward acceleration, a=1.990m/s2
- Electric field strength, E=100N/C
q=(3.11×10−3kg)×(9.81m/s2+1.990m/s2)100N/C
- First, calculate g+a:
g+a=9.81+1.990=11.800m/s2
- Now substitute this back into the equation for q:
q=(3.11×10−3)×(11.800)100
q=0.036758100=3.6758×10−4C
- Convert to microcoulombs:
q=367.58μC≈368μC
- Since the charge must be negative to counteract the downward electric field:
q≈−368μC
The charge that must be placed on the penny is approximately −368μC.
Similar Questions
Figure shows some of the electric field lines due to three point charges q,q2 and q3 of equal magnitude. What are the signs of each of the three charges?
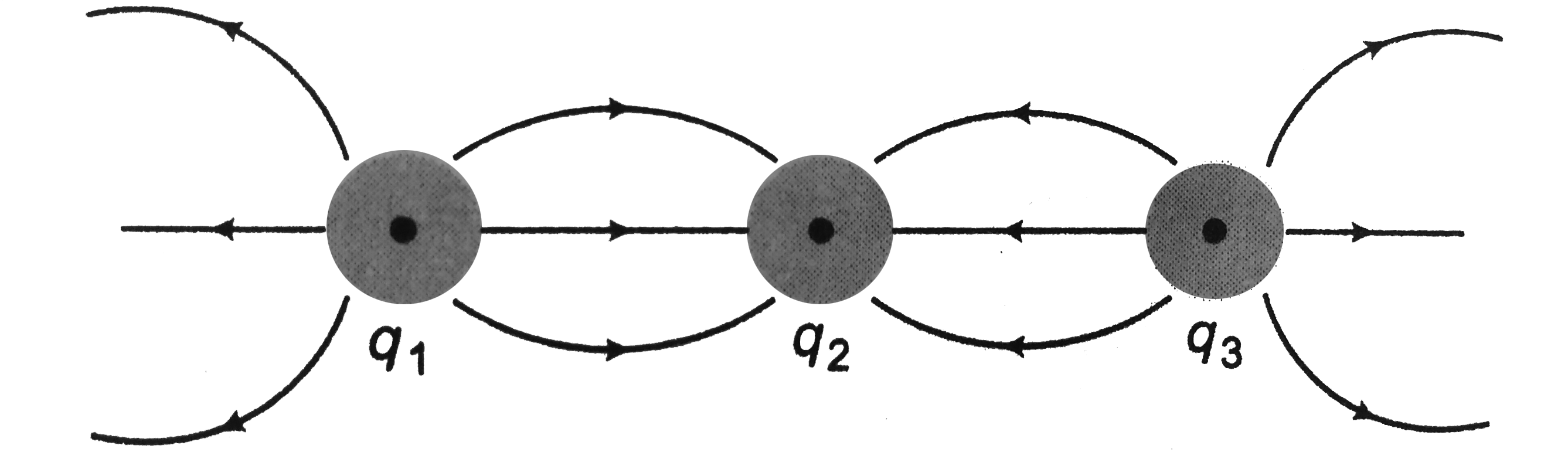
View SolutionFig. shows some of the electric field lines due to three point charges arranged along the vertical axis. All three charges have the same magnitude.
(a) What are the signs of each of the three charges? Explain your reasoning.
(b) At what points(s) is the magnitude of the electric field the smallest? Explain your reasoning. Explain how the fields produced by each individual point charge combine to give a small net field at this point or points.
(c ) Two point charges q and -q are placed at a distance d apart. What are the points at which the resultant electric field is parallel to the line joining the two charge?
 .
.
View SolutionA spherical conductor of radius 10 cm has a charge of 3.2 x 10^-7 C distributed uniformly. What is magnitude of electric field at point 15 cm from centre of sphere?
View SolutionA charge particle is moving with a velocity 3ˆi+4ˆjm/sec and it has electric field E=10ˆkN/C at a given point. Find the magnitude of magneitc field at the same point due to the motion of the charge particle.
View SolutionAnswer the following:
(a) Derive and expression for the electric field at any point on the equatorial line of an electric dipole.
(b) Two identical point charges, q each kept 2m apart in air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
View SolutionTwo blocks of masses 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 m. The upper wire has negligible mass and the lower wire has a uniform mass of 0.2 kg/m. Thewhole system of block, wire and support have an upward acceleration of 0.2 m/s2. g = 9.8 m/s2. The tension at the mid-point of lower wire is-

View SolutionTwo block of mass 2.9kg and 1.9kg are suspended from a rigid support S by two inextensible wires each of length 1m , as shown in figure. The upper wire has negligible mass and the lower wires and support have an uniformly mass of 0.2kg .The whole system of blocks, wire and support have an upwards acceleration of 0.2m/s2. Acceleration due to gravity is 9.8m/s2.
(a) Find the tension at the mid point of the lower wire.
(b)Find the tension at the mid point of the upper wire.

View SolutionThe cube shown in Fig. 2.119 has sides of length L=10.0cm . The electric field is uniform , has a magnitude E=4.00×103NC−1 and is parallel to the xy plane at an angle of 37∘ measured from the +x−aξs toward the +y−aξs .

The surface that have zero flux are
View SolutionA charged cloud system produces an electric field in the air near the earth's surface. A particle of charge −2×10−9 C is acted on by a downward electrostatic force of 3×10−6 N when placed in this field. The gravitational and electrostatic force, respectively, exerted on a proton placed in this field are
View SolutionA uniform ring of mass m is placed on a rough horizontal fixed surface as shown in the figure. The coefficient of friction between the left part of the ring and left part of the horizontal surface is μ1=0.6π and between right half and the surface is μ2=0.2π. At the instant shown, now the ring has been imparted an angular velocity in clockwise sense in the figure shown. At this moment magnitude of acceleration of centre O of the ring (in m/s2) is (take g=10m/s2)

View Solution
