In a region of constant potential,
the electric field is uniform.
the electric field is zero.
there can be no charge inside the region.
both (b) and (c) are correct.
To solve the question regarding the behavior of electric fields in a region of constant potential, we can follow these steps:
1. Understanding Constant Potential:
- In a region of constant potential, the electric potential (V) does not change with position. This means that for any two points in this region, the potential difference (ΔV) is zero.
2. Relation Between Electric Field and Potential:
- The electric field (E) is related to the electric potential (V) by the equation:
E=−dVdr
- Here, dVdr is the gradient of the potential. If the potential is constant, dV=0.
3. Calculating the Electric Field:
- Since dV=0 in a region of constant potential, substituting this into the equation gives:
E=−0dr=0
- Therefore, the electric field in a region of constant potential is zero.
4. Implications of Zero Electric Field:
- If the electric field is zero, it implies that there are no charges present in that region. According to Gauss's law, if the electric field is zero, the net charge enclosed within any closed surface in that region must also be zero.
5. Analyzing the Options:
- Option 1: The electric field is uniform. (Incorrect, as the electric field is zero, not uniform.)
- Option 2: The electric field is zero. (Correct, as derived.)
- Option 3: There can be no charge inside the region. (Correct, as derived from Gauss's law.)
- Option 4: Both B and C are correct. (Correct, since both options 2 and 3 are true.)
6. Conclusion:
- The correct answer is Option 4, as both statements regarding the electric field being zero and the absence of charge inside the region are true.
- In a region of constant potential, the electric potential (V) does not change with position. This means that for any two points in this region, the potential difference (ΔV) is zero.
- The electric field (E) is related to the electric potential (V) by the equation:
E=−dVdr
- Here, dVdr is the gradient of the potential. If the potential is constant, dV=0.
- Since dV=0 in a region of constant potential, substituting this into the equation gives:
E=−0dr=0
- Therefore, the electric field in a region of constant potential is zero.
- If the electric field is zero, it implies that there are no charges present in that region. According to Gauss's law, if the electric field is zero, the net charge enclosed within any closed surface in that region must also be zero.
- Option 1: The electric field is uniform. (Incorrect, as the electric field is zero, not uniform.)
- Option 2: The electric field is zero. (Correct, as derived.)
- Option 3: There can be no charge inside the region. (Correct, as derived from Gauss's law.)
- Option 4: Both B and C are correct. (Correct, since both options 2 and 3 are true.)
- The correct answer is Option 4, as both statements regarding the electric field being zero and the absence of charge inside the region are true.
Topper's Solved these Questions
Similar Questions
(Figure 3.41) shows the lines of constant potential in region in which an electric field is present. The values of potentials are written in brackets. At which points A, B or C, the electric field is greatest.
.
View SolutionAssertion: In parallel combination of electrical appliances, total power consum ption is equal to the sum of the powers of the indivisual appliances.
Reason : Electrons move away from a region of lower potential to a region of higher potential.
View Solution
Knowledge Check
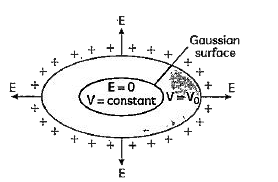
In the region of constant potential:Athe electric field is uniformBthere can be no charge inside the regionCthe electric field is zeroDboth (b) and (c)When a parallel plate capacitor is connected to a source of constant potential difference
Aall the charge drawn from source is stored in the capacitorBthe potential difference across capacitor grows very rapidly initially and this rate decreases to zero eventuallyConly half of the energy drawn from the source is dissipated outside the capacitorDall of theseTwo long coaxial cylindrical metal tubes stand on an insulatiog floor as shown in figure. A dielectric oil is filled in the annular region between the tubes. The tubes are maintained at a constant potential difference V. A small hole is opened at bottom then :
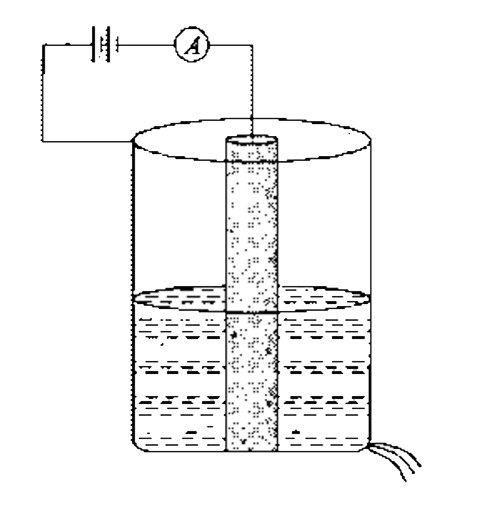AReading of ammeter remain constantBCapacitance of system increasesCCurrent in circuit is dependent on area ofholeDCurrent in circuit is inversely proportional to dielectric constant
A proton and α−partic≤ are accelerated with same potential difference and they enter in the region of constant magnetic field B perpendicular to the velocity of particles. Find the ratio of radius of curvature of alpa−partic≤.
View SolutionIf the length of a potentiometer wire is increased by keeping constant potential difference across the wire, then
View SolutionStatement I: If electric potential in certain region is constant, then the electric field must be zero in this region.
Statement II: →E=−dVdrˆv.
View SolutionAn electron traveling in a uniform electric field passes from a region of potential V1 to a region of higher potential V2. Then
View SolutionA particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=ax2−bx, where a and b are positive constant. The particle will perform.
View Solution