In a game of Archery, each ring of the Archery target is valued. The centremost ring is worth 10 points and rest of the rings are allotted points 9 to 1 in sequential order moving outwards. Archer A is likely to earn 10 points with a probability of 0.8 and Archer B is likely the earn 10 points with a probability of 0.9.
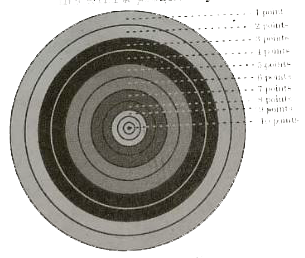
Based on the above information, answer the following questions : If both of them hit the Archery target, then find the probability that:
(a) exactly one of them earns 10 points.
(b) both of them earn 10 points.
Step by step video & image solution for In a game of Archery, each ring of the Archery target is valued. The centremost ring is worth 10 points and rest of the rings are allotted points 9 to 1 in sequential order moving outwards. Archer A is likely to earn 10 points with a probability of 0.8 and Archer B is likely the earn 10 points with a probability of 0.9. Based on the above information, answer the following questions : If both of them hit the Archery target, then find the probability that: (a) exactly one of them earns 10 points. (b) both of them earn 10 points. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION PAPER 2022 TERM 2 SET 3BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 2 SET 3EXERCISE - SECTION C
4 Videos
- QUESTION PAPER 2022 TERM 2 SET 2BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 2 SET 2EXERCISE - Section - C (Case- Study Based Questions)
2 Videos
- QUESTION PAPER 2022 TERM 2 SET 4BOOK - XII BOARDS PREVIOUS YEARCHAPTER - QUESTION PAPER 2022 TERM 2 SET 4EXERCISE - Section -C (Case Study Problem)
2 Videos
Similar Questions
A and B stand in a ring with 10 other persons. If the arrangement of the persons is at random, then the probability that there are exactly 3 persons between A and B is
View SolutionA and B stand in a ring along with 10 other pèrsons. If the arrangement is at random, the probability that there are exactly 3 persons between A and B, is
View Solution
Knowledge Check
A and B stand in a ring along with 10 other persons. If the arrangement is at random, then the probability that there are exactly 3 persons between A and B, is
A111B7324C5162D581Let P be the point (1,0) and Q a point on the locus y2=8x. The locus of mid-point of PQ is :
Ax2−2xy−8=0Bx2+4y+2=0Cy2+4x+2=0Dy2−4x+2=0If the point (1,0),(0,1)and(x,8) are collinear, then the value of x is equal to
A5B−6C6D−7
The probability that a bomb will hit a target is 0.8 Find the probability that out of 10 bombs dropped.exactly 4 will hit the target .
View SolutionA and B stand around a ring with 10 other people. If the probability that there are exactly 3 persons between A and B is m find 1m .
View SolutionAn artillery target may be either at point I with probability 8/9 or at point II with probability 1/9 we have 55 shells, each of which can be fired either rat point I or II. Each shell may hit the target, independent of the other shells, with probability 1/2. Maximum number of shells must be fired a point I to have maximum probability is 20 b. 25 c. 29 d. 35
View SolutionAn artillery target may be either at point A with probability 89 or at point B with probability 19, we have 21 shells, each of which can be fired either at point A or at point B. Each shell may hit the target independently of the other shells, with probability 12 How may shells must be fired at point A to hit the target with maximum probability ?
View SolutionThe probability of hitting a target in any shot is 0.2 If 10 shorts are fired , find the probability that the target will be hit at least twice. [ Given: (0.8)9=0.1342]
View Solution
