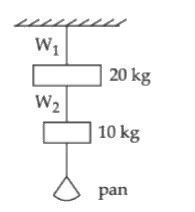
Wires W1 and W2 are made of same material having the breaking stress of 1.25×109N/m2.W1andW2 have cross-sectional area of 8×10−7m2and4×10−7m2, respectively. Masses of 20 kg and 10 kg hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is kg. (Use g=10m/s2)
The correct Answer is:40
σ1=(m+30)g8×10−7=1.25×109
⇒m=30=100
m= 70
σ2=(m+10)g4×10−7=1.25×109
m+10=50
m= 40
⇒40 kg is safest maximum mass.
Similar Questions
A body of mass m = 10 kg is attached to a wire of length 0.3m. The maximum angular velocity with which it can be rotated in a horizontal circle is (Given, breaking stress of wire = 4.8 xx 10^(7) Nm^(-2) and area of cross-section of a wire = 10^(-6) m^(2) )
View SolutionA stress of 10^7 N m^-2 is required to break a material of density 4 xx 10^4 kg m^-3 . Calculate the length of a wire of this material, which can break under its own weight.
View Solutionଏକ ଧାତବ ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ 4×10−8m2 ଓ ବିଶିଷ୍ଟ ପ୍ରତିରୋଧ 10×10−8Ωm | ଏହାର ପ୍ରତିରୋଧ 25Ωହେଲେ ଦୈର୍ଘ୍ୟ କେତେ ହେବ ?
View SolutionThe area of a wire's width 4 times 10^(-8)M^2 And one of the prominent resistances 10 times 10^(-8) Omega M | This wire resistance 25 Omega However, its length will be ____
View SolutionFind the resistance (in mega Ω) of a wire of length 10 m, cross sectional area 1cm2 and made of a material of resistivity 100 Ωm.
View SolutionTwo blocks of masses 5 kg and 10 kg are connected by a metal wire which passes through a smooth pulley as shown in the figure. breaking stress of metal wire 2 xx 10^(9) N m^(-2) Is. If g = 10 m s^(-2) , then what is the minimum radius of the wire which will not break?
View Solutionwires made of similar material W_(1) And W_(2) dissipative counterpart of 1.25xx10^(9)N//m^(2) Is. W_(1) And W_(2) area of cross section of 8xx10^(-7)मी^(2) And 4xx10^(-7)मी^(2) Is. Masses of 20 kg and 10 kg are suspended from them as shown in the figure, the maximum mass that can be placed on the pan without breaking the wires is ............... .. is kg. ( g=10मी/से^(2) use)
View SolutionWires W1 and W2 are made of same material having the breaking stress of 1.25×109N/m2.W1andW2 have cross-sectional area of 8×10−7m2and4×10−7m2, respectively. Masses of 20 kg and 10 kg hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is kg. (Use g=10m/s2)

View Solution
