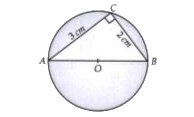
In the given figure, AOB is a diameter of the circle with centre at 'O' and ∠ADC=125∘ then ∠BAC is:

A
35∘
B
45∘
C
55∘
D
65∘
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - EXERCISE (ASSERTION & REASON TYPE)
4 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - EXERCISE (COMPREHENSION TYPE)
3 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - NCERT SECTION (EXERCISE 10.6)
2 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Olympiad/HOTS Corner
14 Videos
- CONSTRUCTIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONSTRUCTIONS EXERCISE - OLYMPIAD/HOTS CORNER
5 Videos
Similar Questions
Knowledge Check
In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
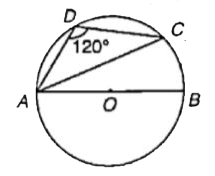 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determinedIn the given figure O is the centre of the circle and ∠BAC=25∘, then the value of ∠ADB is :
 A40∘B55∘C50∘D65∘
A40∘B55∘C50∘D65∘In the given figure, O is the centre of the circle and ∠AOC=100∘. Find the ratio of ∠ADC:∠ABC :
 A5:6B1:2C5:13Dnone of the above
A5:6B1:2C5:13Dnone of the above
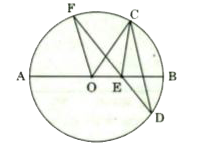
In the figure given below, AB is the diameter of the circle whose centre is at O. Given that ∠ECD=∠EDC=32∘, then ∠CEFand∠COF respectively are
View SolutionIn the given figure O is the centre of the circle and AB||CD. If ∠ADC=25∘, then find ∠AEB∘-

View SolutionIn the given figure , AD is a diameter O is the centre of the circle AD is parallel to BC and ∠CBD=32∘
(i) ∠OBD
(ii )∠AOB
(iii) ∠BED

View SolutionABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC=150∘. Then. ∠BAC is equal to:
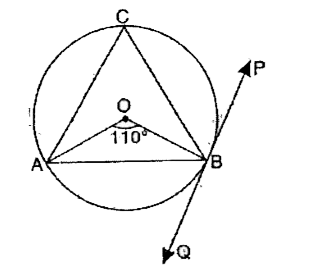
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
View Solution