ABCD is a cyclic quadrilateral such that side AB is the diameter of the circle and ∠ADC=140∘. The value of ∠BAC is:
40∘
45∘
50∘
60∘
The correct Answer is:C
Topper's Solved these Questions
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - EXERCISE (COMPREHENSION TYPE)
3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Olympiad/HOTS Corner
14 Videos
- CONSTRUCTIONS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONSTRUCTIONS EXERCISE - OLYMPIAD/HOTS CORNER
5 Videos
Similar Questions
In the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.
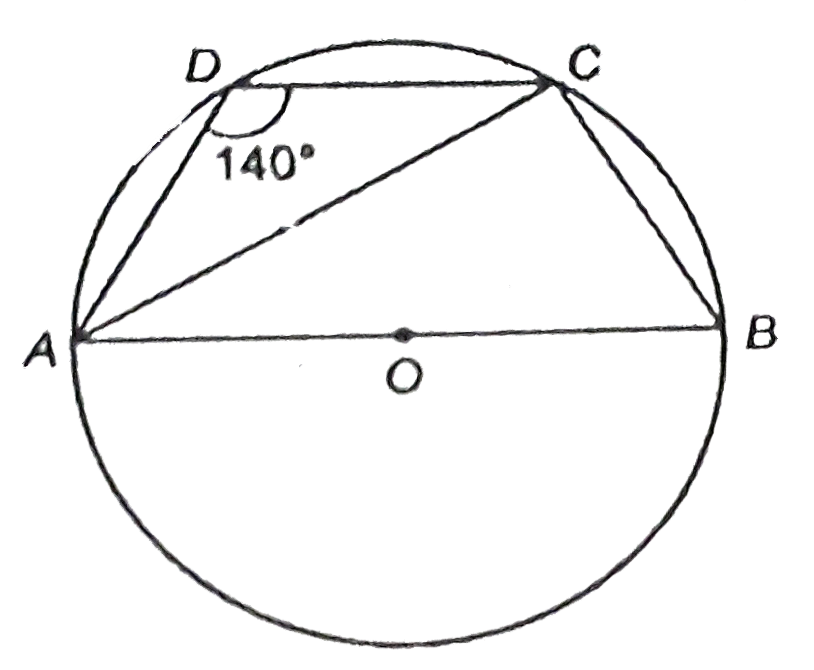
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

View Solution
Knowledge Check
ABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC=150∘. Then. ∠BAC is equal to:
A40∘B60∘C38∘D50∘ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
A80∘B50∘C40∘D30∘ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC = 140∘, ∠BAC is equal to:
ABCD एक चक्रीय चतुर्भज है जो इस प्रकार है कि AB इसे घेरने वाले वृत्त का व्यास है तथा कोण ADC = 140∘, है | कोण ∠BAC किसके बराबर है?A38∘B40∘C50∘D60∘
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
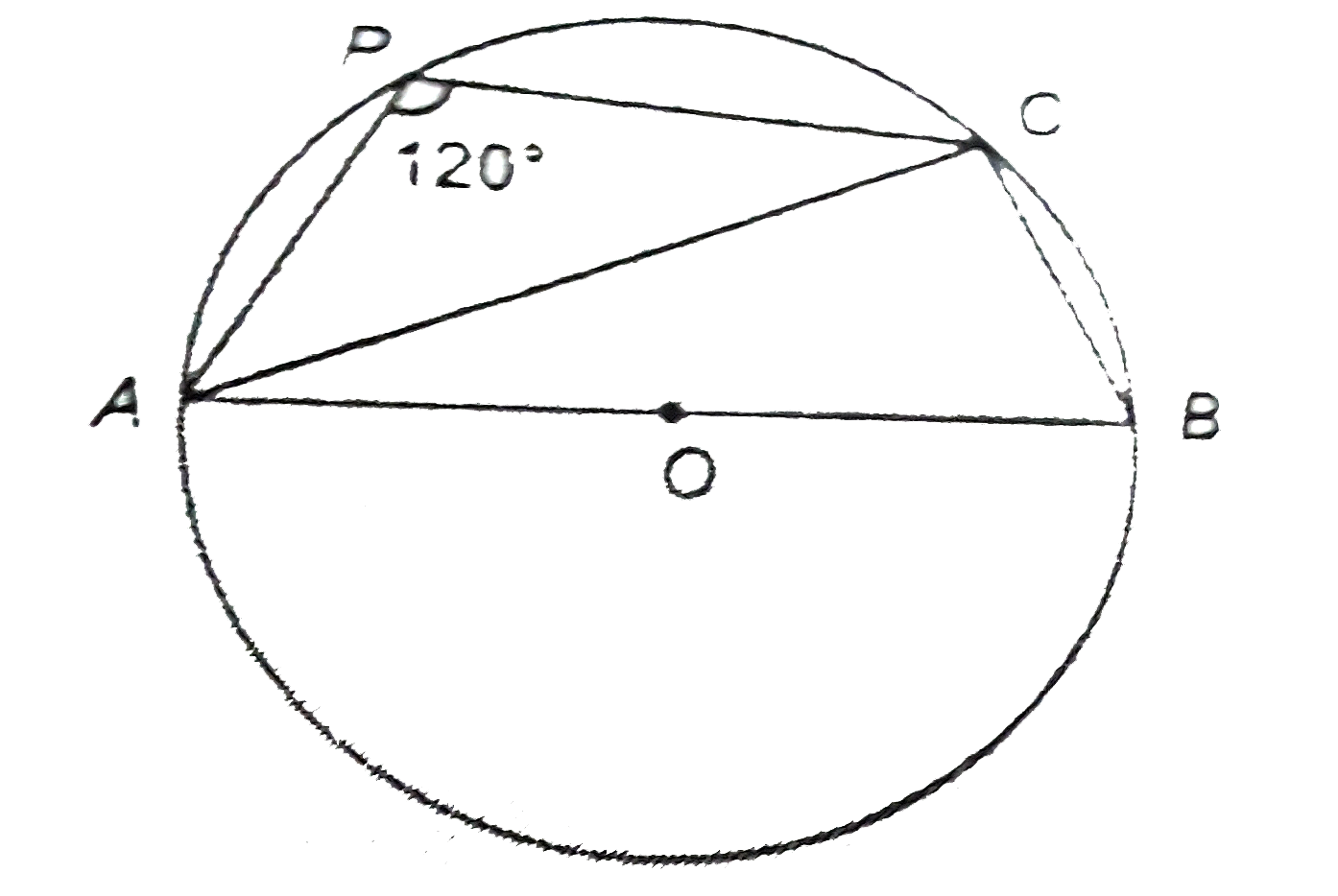
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.

View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and angle ADC=130∘ . Then angle BAC is equal to:
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, then ∠BAC is equal to
View Solution
