The area of a parallelogram ABCD in which AB= 12 cm, BC= 9 cm and diagonal AC= 15 cm is k cm2. The value of k is
The correct Answer is:k=108 cm
Topper's Solved these Questions
- HERON'S FORMULABOOK - MTG IIT JEE FOUNDATIONCHAPTER - HERON'S FORMULAEXERCISE - OLYMPIAD/HOTS CORNER
7 Videos
- HERON'S FORMULABOOK - MTG IIT JEE FOUNDATIONCHAPTER - HERON'S FORMULAEXERCISE - EXERCISE (SUBJECTIVE TYPE)
17 Videos
- FOOTSTEPS TOWARDS CBSE BOARDBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS CBSE BOARDEXERCISE - PART-B (SECTION-IV)
4 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - OLYMPIAD/HOTS CORNER
5 Videos
Similar Questions
Knowledge Check
Find the area of a parallelogram ABCD in which AB = 8 cm, BC = 15 cm and diagonal AC = 17 cm.
A220cm2B150cm2C120cm2D175cm2ABCD is a parallelogram with sides AB = 12 cm, BC= 10 cm and diagonal AC = 16 cm. The area of the parallelogram and the distance between the shorter sides are respectively.
A120.5cm2,12.05cmB119.8cm2,11.98cmC118.71cm2,11.87cmD117.9cm2,11.79cm
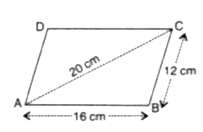
In parallelogram ABCD, AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram.
View SolutionConstruct a parallelogram ABCD with AB=5cm, BC=4.5cm, and AC=7cm.
View SolutionFind the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm.
View SolutionFind the area of a quadrilateral ABCD in which AB=3 cm, BC=4 cm, CD=4 cm, DA=5 cm and AC=5 cm
View SolutionFind the area of a quadrilateral ABCD is which AB=3cm, BC=4cm, CD=4cm, DA=5cm and AC=5cm
S=12(a+b+c)=12(3+4+5)=6
arof ABC=sqrt(s(s-a)(s-b)(s-c)<br>ar ABC=√6(6−3)(6−4)(6−5)
⇒√6×3×2×1=6cm2
Now in △ADC,S=a+b+c2
⇒s=5+4+52=142=7cm
By using Heron’s formula
Area of △ADC=√s(s−a)(s−b)(s−c)
=√7(7−5)(7−4)(7−5)
=√7×2×3×2
=2√21cm2
Area of△ADC=9.2cm2 (approx.)
Area of the quadrilateral ABCD = Area of △ADC+Areaof△ABC=9.2cm2+6cm2=15.2cm2
Thus, the area of the quadrilateral,ABCDis15.2cm2.
View SolutionFind the area of the quadrilateral ABCD in which AB=3cm,BC=4cm,CD=4cm,DA=5cm and AC=5cm.
View Solution
