In an acitivity class, students were asked to make a circular rangoli. Trishu, Sidak, Mini and Kavleen made rangolis having different diameters as 1720 inches, 34 inches, 56 inches and 710 inches, respectively. Who among them made the smallest rangoli?
Kavleen
Trishu
Mini
Sidak
The correct Answer is:A
Topper's Solved these Questions
- FRACTIONSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FRACTIONSEXERCISE - EXERCISE SUBJECTIVE PROBLEMS ( Integer /Numerical Value Type)
6 Videos
- DECIMALSBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DECIMALSEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
- INTEGERS BOOK - MTG IIT JEE FOUNDATIONCHAPTER - INTEGERS EXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
Level-3 11. On Vanmahotsva day, students of class IX were asked to get saplings & develop nursery in the triangular region allotted to them as in the figure given below: A 2 3 4 5 6 7 8 9 10 (i) Find the coordinates of the vertices P, Q, R (ii) Find the area in which the nursery has been developed
View SolutionProfessor Malingowski, a chemist and teacher at to communite college, is organizing his graduated cylinders in the hopes of keeping his office tidy and setting a good example for his students. He has beakers with diameters, in inches, of 12,34,45,1 and 54.
With his original five cylinders, Professor Malingowski realizes that he is missing a cylinder necessary for his upcoming lab demonstration for Thurday's class. He remembers that the cylinder the needs, when added to the original five, will create a median diameter value of 910 for the set of six total cylinders. He also knows that the measure of the sixth cylinder will exceed the value of the range of the current five cylinders by a width of anywhere from 14 inches to 12 inches, inclusive. Based on the above data, which is one possible value of y, the diameter of this missing sixth cylinder?
View Solution
Knowledge Check
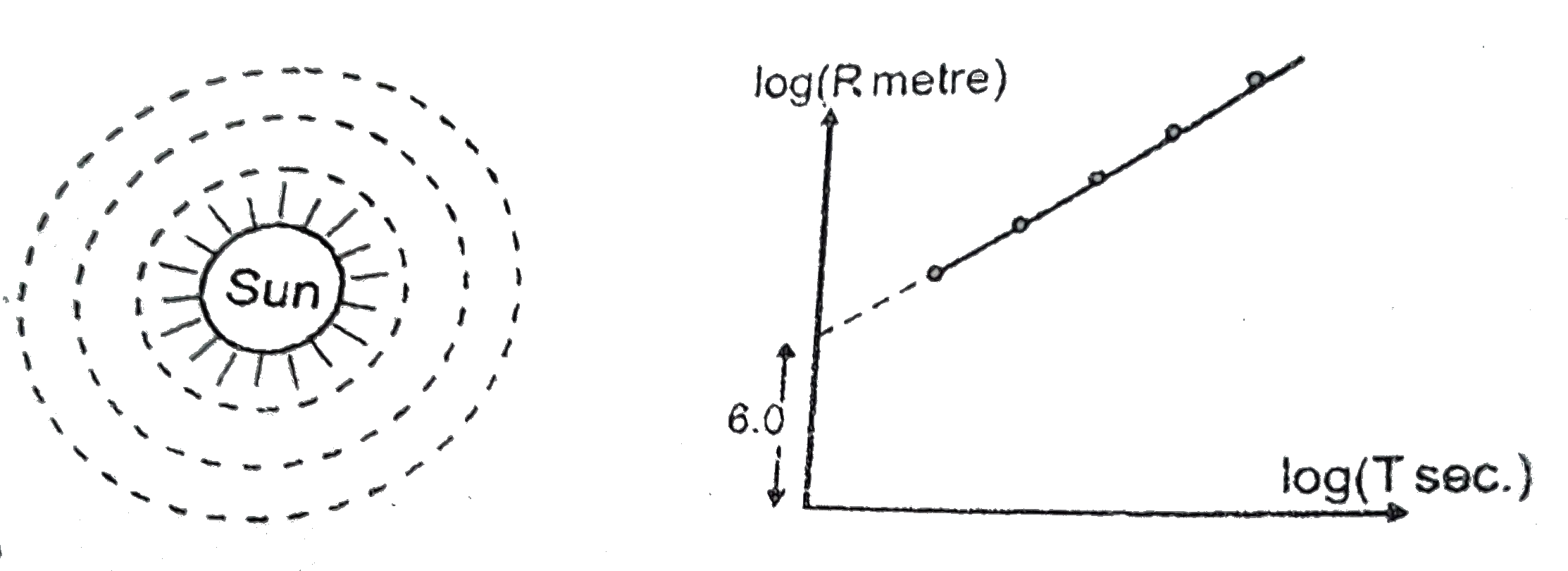
Many planets are revolving around the fixed sun in circular orbits of different radius (R) and difference time period (T) To estimate the mass of the sun the orbital radius (R) and time period (T) of planets were noted. Then log10 T v/s log10R curve was plotted.
The curve was found to be approximately straight line (as shown in) having y intercept =6.0 (Neglect the gravitational interaction among the planets) [Take G=203×10−11 in MKS, π2=10]
Two plantes A and B having orbital radius R and 4R are initally at the closest position and rotating in the same direction if angular velocity of planet B is ω0 then after how much time will both the planets be again in the closest postion? (Neglect the interaction between planets)
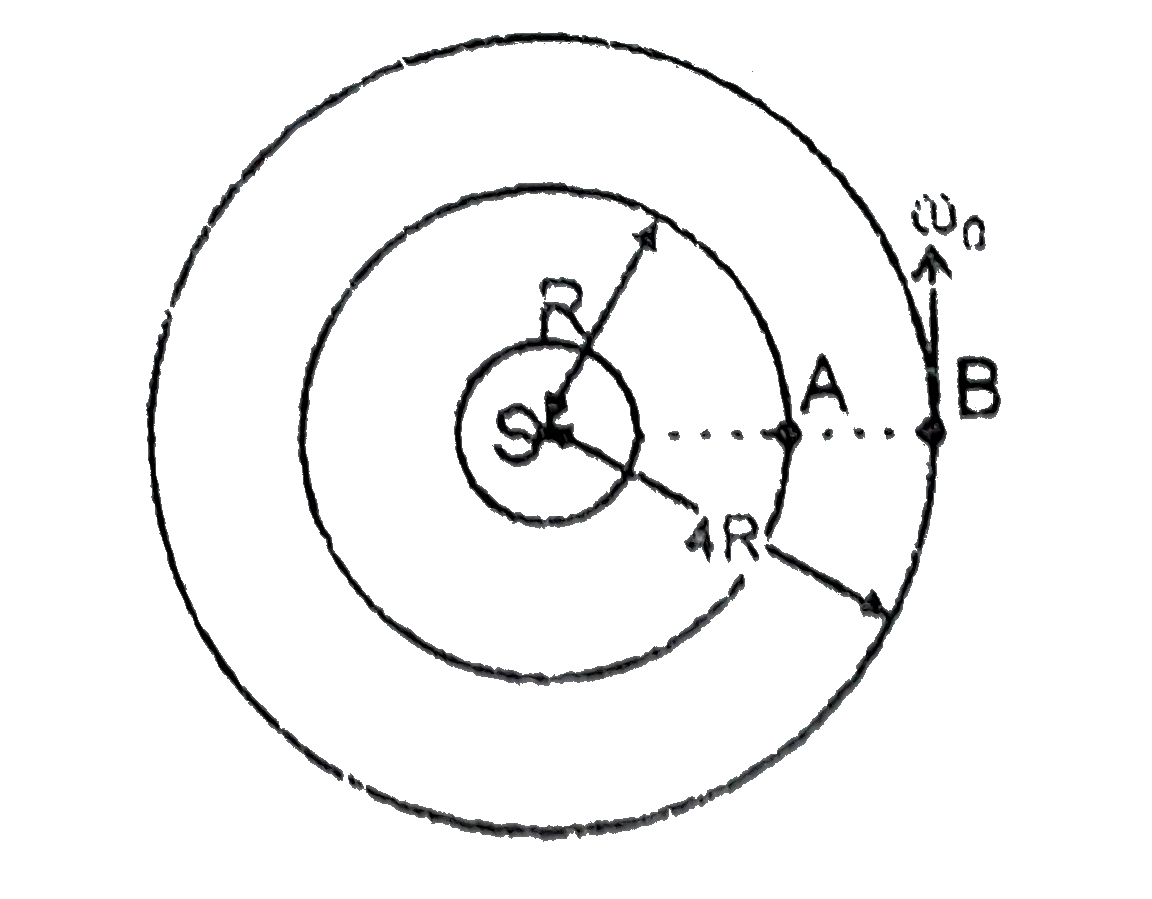 .A2π7ω0B2π9ω0C2πω0D2π5ω0
.A2π7ω0B2π9ω0C2πω0D2π5ω0The alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at 20∘C are 1×10−7and3×10−5Ωm and their temperature coefficient of resistance are 5×10−3∘Cand−7.5×10−4∘C, respectively. Thermal expansion is neglected. Here, △R1+△R2=0 (where △R1and△R2 are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
Ratio of heat produced in them isA0.51B1C0.15D2The alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at 20∘C are 1×10−7and3×10−5Ωm and their temperature coefficient of resistance are 5×10−3∘Cand−7.5×10−4∘C, respectively, Thermal expansion is neglected. Here, △R1+△R2=0 (where △R1,and△R2, are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
Ratio of heat produced in them isA0.51B1C0.15D2
Professor Malingowski, a chemist and teacher at to communite college, is organizing his graduated cylinders in the hopes of keeping his office tidy and setting a good example for his students. He has beakers with diameters, in inches, of 12,34,45,1 and 54.
Professor Malingowski notices one additional cylinder lying on the ground, and can recall certain facts about it, but not its actual diameter. If he knows that the value of the additional graduated cylinder's diameter ,x, will not create any modes and will make the mean of the set equal to 56, what is the value of the additional cylinder's diameter?
View SolutionA psychologist selected a random sample of 20 students. He grouped them in 10 pairs so that the students in each pair have nearly equal scores in an intelligence test. In each pair, one student was taught by method A and the other by method B and examined after the course. The marks obtained by them after the course are as follows.
PairsMethod AMethod B134382364332839434455404363050734528283993240104242 Calculate spearman's Rank correlation
View SolutionThe alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at 20∘C are 1×10−7and3×10−5Ωm and their temperature coefficient of resistance are 5×10−3∘Cand−7.5×10−4∘C, respectively. Thermal expansion is neglected. Here, △R1+△R2=0 (where △R1and△R2 are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
A copper wire is stretched to make it 1% longer. The percentage change in its resistance is
View SolutionThe alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at 20∘C are 1×10−7and3×10−5Ωm and their temperature coefficient of resistance are 5×10−3∘Cand−7.5×10−4∘C, respectively, Thermal expansion is neglected. Here, △R1+△R2=0 (where △R1,and△R2, are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
Ratio of their thickness is
View SolutionThe alternate discs of iron and carbon, having same area of cross-section are cemented together to make a cylinder whose temperature coefficient of resistivity is zero. The change in temperature in two alternate discs is same. The ratio of their thickness and ratio of heat produced in them is found out. The resistivity of iron and carbon at 20∘C are 1×10−7and3×10−5Ωm and their temperature coefficient of resistance are 5×10−3∘Cand−7.5×10−4∘C, respectively. Thermal expansion is neglected. Here, △R1+△R2=0 (where △R1and△R2 are the increase in resistances of iron and carbon, respectively, with the rise in temperature) because combined temperature coefficient of resistivity is given as zero.
Ratio of their thickness is
View Solution
