ΔABC is isosceles with AB=AC=7.5mandBC=9cm The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
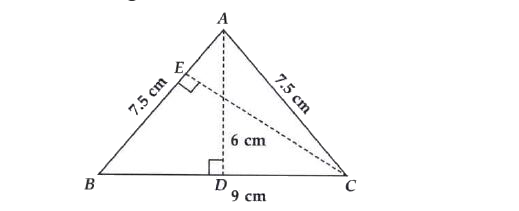
The correct Answer is:7.2cm
Topper's Solved these Questions
- PERIMETER AND AREA BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - NCERT SECTION (EXERCISE 10.3)
20 Videos
- PERIMETER AND AREA BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - NCERT SECTION (EXERCISE 10.4)
18 Videos
- PERIMETER AND AREA BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PERIMETER AND AREA EXERCISE - NCERT SECTION (EXERCISE 10.1)
8 Videos
- LINES AND ANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLES EXERCISE - OLYMPIAD / HOTS CORNER
2 Videos
- PREP TEST 1 BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST 1 EXERCISE - SECTION-B
29 Videos
Similar Questions
ΔABC is isosceles with AB=AC=7.5cmandBC=13cmandAC=12cm. The height AD from A to BC is 6cm. Find the area of ΔABC. What will be the height from C to AB,CE
View SolutionΔABC is isosceles with AB=AC=7.5cmandBC=9cm. The height AD from A to BC is 6cm. Find the area of ΔABC. What will be the height from C to AB,CE
View Solution
Knowledge Check
△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
A9 cmB12 cmC18 cmD20 cm
EXAMPLE 12 Triangle ABC is isosceles with AB=AC=7.5cmandBC=9cm. The height from A to BC i.e. AD is 6 cm. Find the area of ΔABC. What will be the height from C to AB ?
View SolutionΔABC is isosceles with AB=AC=7cm and BC=9cm. The height AD from A to BC, is 6cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?
View SolutionTriangle ABC is isosceles with AB=AC=7.5 cm and BC=9 cm . The height from A to BC i.e, AD is 6 cm. Find the area of ABC. what will be the height from C to AB?
View SolutionΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionABC is an isosceles triangle with AB = AC =13 cm and BC = 10 cm. Calculate the length of the perpendicular from A to BC.
View SolutionIn △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View Solution
