Doubtnut Promotions Sticky

Fill in the blanks.
(i) P and Q are the end points of the diameter of a circle, having its centre at R. If the coordinates of P and Q are respectively (−3,3)and(5,1), then the coordinates of R are ______ .
(ii) If the point C(-1, 2) divides internally the line segment joining A(2, 5) and Bin the ratio 3: 4, then the coordinates of B are _______.
(iii) If the points A(1,2),B(0,0)andC(a,b) are collinear, then __
(iv) The points (−4,0),(4,0)and(0,3) are the vertices of a/an __ .
Fill in the blanks. (i) P and Q are the end points of the diameter of a circle, having its centre at R. If the coordinates of P and Q are respectively (-3, 3) and (5, 1), then the coordinates of R are . (ii) If the point C(-1, 2) divides internally the line segment joining A(2, 5) and Bin the ratio 3: 4, then the coordinates of B are . (iii) If the points A(1, 2), B(0, 0) and C(a, b) are collinear, then (iv) The points (-4, 0), (4, 0) and (0, 3) are the vertices of a/an .

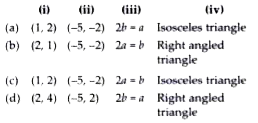
Text Solution
Verified by Experts

The correct Answer is:C

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 10MATHSCOORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    If the point R(1, -2) divides externally the line segment joining P(2, 5) and Q in the ratio 3 : 4, what will be the coordinates of Q?

    A(- 3, 6)
    B(2, - 4)
    C(3, 6)
    D(1, 2)
  • Question 2 - Select One

    What are the coordinates of the point c, such that B(12,6) divides the line segment joining the points A(3, 5) and C in the ratio of 1 : 3 ?

    A(0, 0)
    B(7, 9)
    C(7, -9)
    D(-7, 9)
  • Question 3 - Select One

    The coordinates of the point P dividing the line segment joining the points A(1, 3) and B(4, 6) in the ratio 2:1 is

    A(2, 4)
    B(3, 5)
    C(4, 2)
    D(5, 3)