A small ball of mass m is thrown upward with velocity u from the ground. The ball experiences a resistive force $m k v^{2}$ where v is its speed. The maximum height attained by the ball is :

A

$\frac{1}{2 k} {tan}^{- 1} \frac{k u^{2}}{g}$

B

$\frac{1}{k} ln (1 + \frac{k u^{2}}{2 g})$

C

$\frac{1}{k} {tan}^{- 1} \frac{k u^{2}}{2 g}$

D

$\frac{1}{2 k} ln (1 + \frac{k u^{2}}{g})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$\to F = m k v^{2} - m g$
$\to a = \frac{\to F}{m} = - [k v^{2} + g]$
$\Rightarrow v . \frac{d v}{d h} = - [k v^{2} + g]$
$\Rightarrow 0 \int u \frac{v . d v}{k v^{2} + g} = - H \int 0 d h$
$\frac{1}{2 K} {ln [k v^{2} + g]}_{u}^{0} = - H$
$\Rightarrow \frac{1}{2 K} ln [\frac{k u^{2} + g}{g}] = H$
$= \frac{1}{2 K} ln [1 + \frac{k u^{2}}{g}]$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

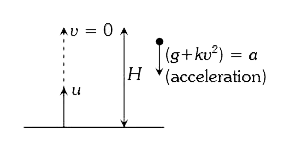
Similar Questions

Recommended Questions

Home
Ask Doubt
Profile