Assertion- adiabatic process work done by the gas W=nRT1−γ
Reason- if work is done on gas temperature will increase.
To analyze the given assertion and reason, we will break down the concepts of adiabatic processes and the relationship between work done, internal energy, and temperature changes.
1. Understanding the Assertion:
The assertion states that the work done by the gas during an adiabatic process can be expressed as:
W=nRT1−γ
where n is the number of moles, R is the universal gas constant, and γ (gamma) is the ratio of specific heats (Cp/Cv).
Hint: Recall the definitions of Cp and Cv and how they relate to γ.
2. Analyzing the Adiabatic Process:
In an adiabatic process, there is no heat exchange with the surroundings, which means Q=0. According to the first law of thermodynamics:
ΔU=Q−W
Since Q=0, we have:
ΔU=−W
Hint: Remember that for an ideal gas, the change in internal energy ΔU can be expressed in terms of temperature change.
3. Relating Work Done to Temperature Change:
For an ideal gas, the change in internal energy can also be expressed as:
ΔU=nCvΔT
Combining this with our previous equation, we can write:
−W=nCvΔT⇒W=−nCvΔT
This indicates that if work is done on the gas (compressing it), the internal energy increases, leading to an increase in temperature.
Hint: Consider how work done on the gas affects its internal energy and temperature.
4. Understanding the Reason:
The reason states that if work is done on the gas, the temperature will increase. This is indeed true because when work is done on the gas, it compresses and increases its internal energy, resulting in a temperature rise.
Hint: Think about the relationship between work, internal energy, and temperature in the context of the first law of thermodynamics.
5. Conclusion on Assertion and Reason:
Both the assertion and the reason are true statements. However, the assertion's formula is not universally applicable as it is derived under specific conditions. The reason correctly explains the effect of work done on the gas.
Hint: Evaluate the correctness of statements based on their definitions and contexts.
Final Answer:
- Assertion: True (but context-specific).
- Reason: True.
- Conclusion: Both statements are true, but the assertion is not universally applicable without context.
The assertion states that the work done by the gas during an adiabatic process can be expressed as:
W=nRT1−γ
where n is the number of moles, R is the universal gas constant, and γ (gamma) is the ratio of specific heats (Cp/Cv).
In an adiabatic process, there is no heat exchange with the surroundings, which means Q=0. According to the first law of thermodynamics:
ΔU=Q−W
Since Q=0, we have:
ΔU=−W
For an ideal gas, the change in internal energy can also be expressed as:
ΔU=nCvΔT
Combining this with our previous equation, we can write:
−W=nCvΔT⇒W=−nCvΔT
This indicates that if work is done on the gas (compressing it), the internal energy increases, leading to an increase in temperature.
The reason states that if work is done on the gas, the temperature will increase. This is indeed true because when work is done on the gas, it compresses and increases its internal energy, resulting in a temperature rise.
Both the assertion and the reason are true statements. However, the assertion's formula is not universally applicable as it is derived under specific conditions. The reason correctly explains the effect of work done on the gas.
- Assertion: True (but context-specific).
- Reason: True.
- Conclusion: Both statements are true, but the assertion is not universally applicable without context.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The work done in adiabatic process is given by
AnR(T1)−T2γBnR(T1)−T2γ−1C(nR(T1)−T2)RDγ(T1)−T2RnAssertion: In adiabatic process work is independent of path.
Reason: In adiabatic process work done is equal to negative of change in internal energy.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reson are true but reason is not the correct explanation of assertion.Cif assertion is true but reason is false.DIf both assertion and reason are false.In an adiabatic process 90 J of work is done on the gas. The change in internal energy of the gas is
A−90jB+90jC0 jDDepends on initial temperature
A cylinder containing a gas is lifted from the first floor to the second floor. What is the amount of work done on the gas? What is the amount of work done by the gas? Is the internal energy of the gas increased ? Is the tempreture of the gas increased?
View SolutionFind work done by the gas in the process shown in figure :
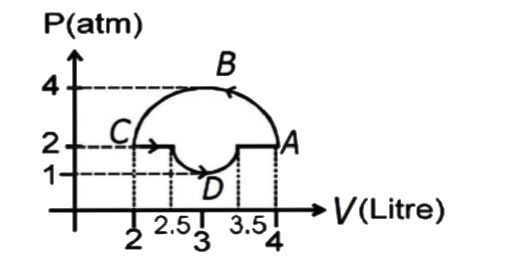
View SolutionFind work done by the gas in the process shown in figure.

View SolutionFind the work done by the gas in the process ABC.
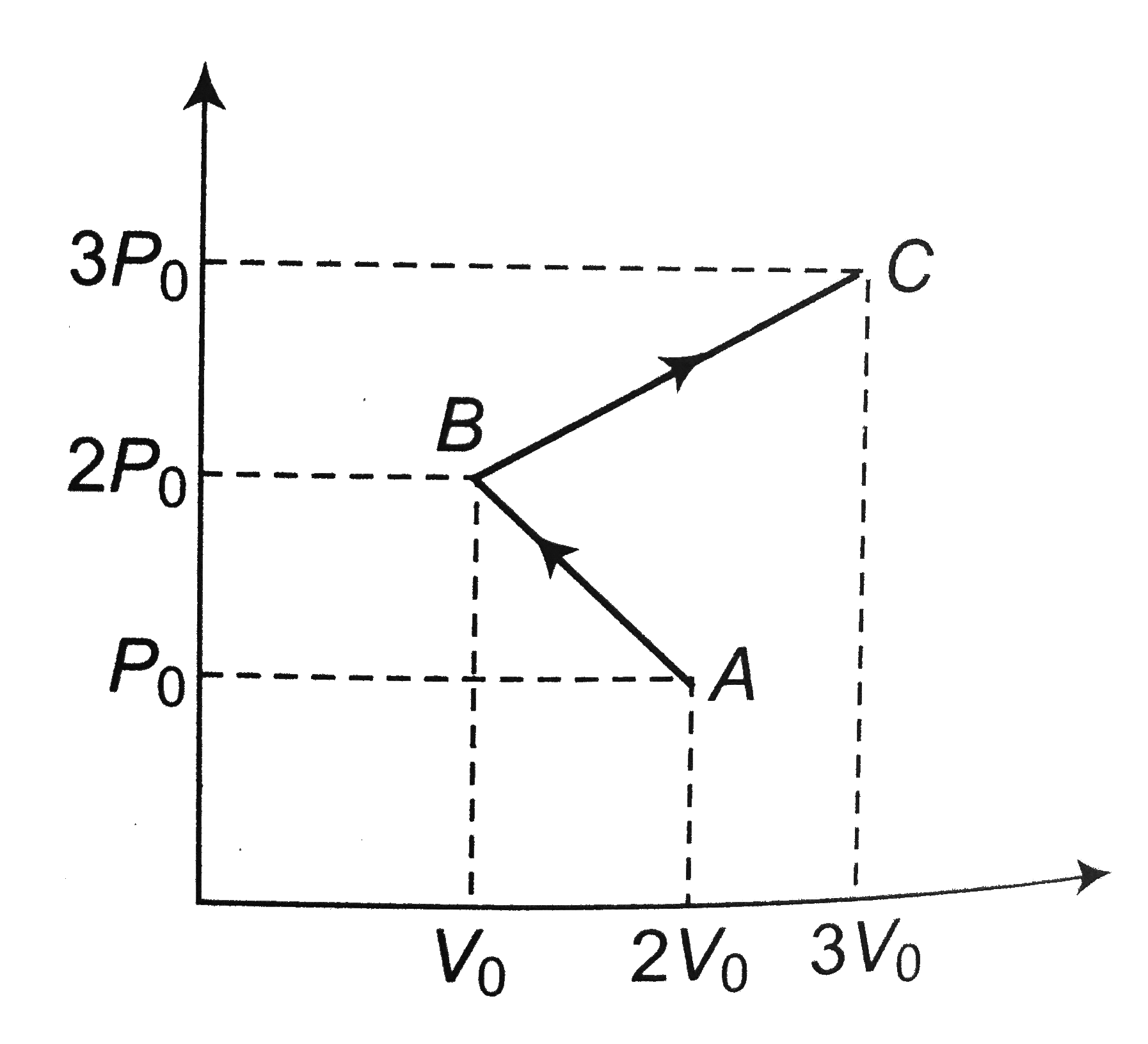
View SolutionOne mole of ideal gas is allowed to expand reversibly and adiabatically from a temperature of 27∘C. If the work done by the gas in the process is 3 kJ, the final temperature will be equal to (Cv=20J/Kmol)
View Solution
