For 2 mole pf an ideal mono atomic gas at 300K calculate internal energy ?
To calculate the internal energy of 2 moles of an ideal monoatomic gas at 300 K, we can follow these steps:
Step 1: Understand the formula for internal energy
The internal energy (U) of an ideal monoatomic gas can be calculated using the formula:
U=32nRT
where:
- U = internal energy
- n = number of moles of the gas
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
Step 2: Identify the values
From the question, we have:
- Number of moles n=2 moles
- Temperature T=300 K
- Gas constant R=8.314 J/(mol·K)
Step 3: Substitute the values into the formula
Now, we can substitute the values into the formula:
U=32×2×8.314×300
Step 4: Calculate the internal energy
Now, let's perform the calculations step by step:
1. Calculate 32×2=3
2. Calculate 3×8.314=24.942
3. Now multiply by the temperature: 24.942×300=7482.6 J
Step 5: Round the result
The internal energy can be rounded to:
U≈7483 J
Final Answer
The internal energy of 2 moles of an ideal monoatomic gas at 300 K is approximately 7483 J.
---
The internal energy (U) of an ideal monoatomic gas can be calculated using the formula:
U=32nRT
where:
- U = internal energy
- n = number of moles of the gas
- R = universal gas constant (8.314 J/(mol·K))
- T = temperature in Kelvin
From the question, we have:
- Number of moles n=2 moles
- Temperature T=300 K
- Gas constant R=8.314 J/(mol·K)
Now, we can substitute the values into the formula:
U=32×2×8.314×300
Now, let's perform the calculations step by step:
1. Calculate 32×2=3
2. Calculate 3×8.314=24.942
3. Now multiply by the temperature: 24.942×300=7482.6 J
The internal energy can be rounded to:
U≈7483 J
The internal energy of 2 moles of an ideal monoatomic gas at 300 K is approximately 7483 J.
Topper's Solved these Questions
Similar Questions
One mole of an ideal monoatomic gas at 1 atm, 300 K undergo a process in which pressure of gas is 8 atm then calculate W (in cal).
View SolutionAt constant volume 4 mol of an ideal gas when heated form 300k to 500k changes its internal energy by 500 J . The molar heat capacity at constant volume is ________.
View Solution
Knowledge Check
Two moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
A179 KB189 KC199 KD219 KIn a constant pressure process, for 5mole of an ideal monoatomic gas, the temperature of gas increased form 300K→500k. Which of the following is incorrect reagarding the process?
AδHsys=2500RBδUsys=1500RCQ=3500RDω=−1000RAt constant volume , 4 moles of an ideal gas when heated from 300 K to 500 K change its internal energy by 5000 J. The molar heat capacity at constant volume is ?
A3.125B6.25C6.75D−6.75
2 moles of an ideal mono atomic gas undergoes reversible expansion from (4L,[400K) to 8L such that TV2=constant The change in enthalpy of the gas is
View SolutionCalculate the internal energy of one mole of a diatomic gas at 300 K. Assume the molecules to be rigid.
View SolutionAt 27∘C two moles of an ideal monatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate
(a) final temperature of the gas
(b) change in its internal energy and
(c) the work done by the gas during the process. [ R=8.31J/mol−K]
View Solution3 moles of an ideal mono atomic gas performs a cycle as shown in fig. If gas temperature TA=400K TB=800K,TC=2400K, and TD=1200K. Then total work done by gas is
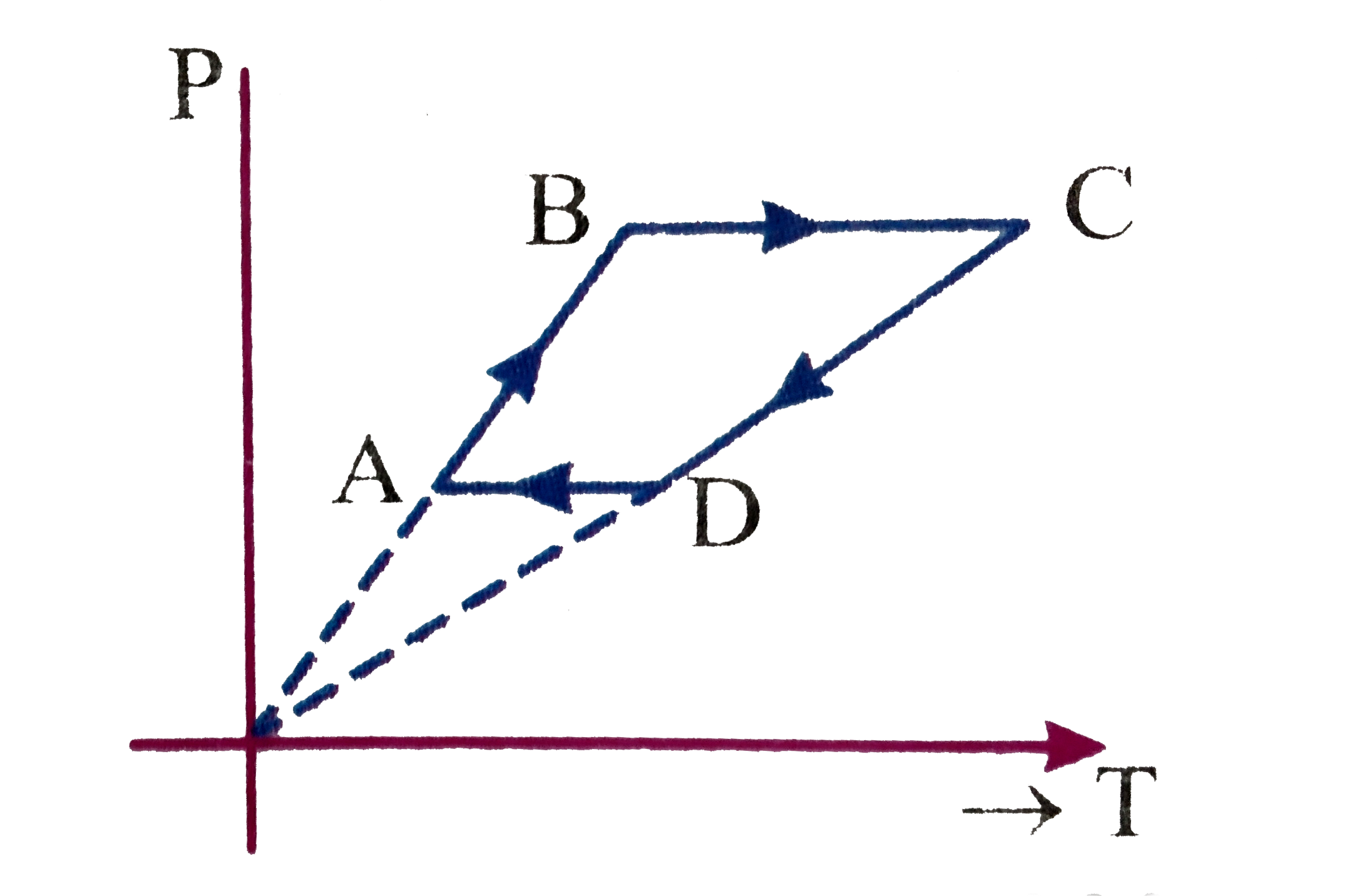
View SolutionOne mole of an ideal mono-atomic gas is caused to go through the cycle shown in the figure below. Then the change in the internal enegry in expanding the gas from a to c along the path abc is:

View Solution
