Two masses m1=1kgandm2=2kg are connected by a light inextensible string and suspended by means of a weightness pulley as shown in the figure. Assuming that both the masses start from rest, the distance travelled by the centre of mass in two seconds is (Takeg=10ms−2.
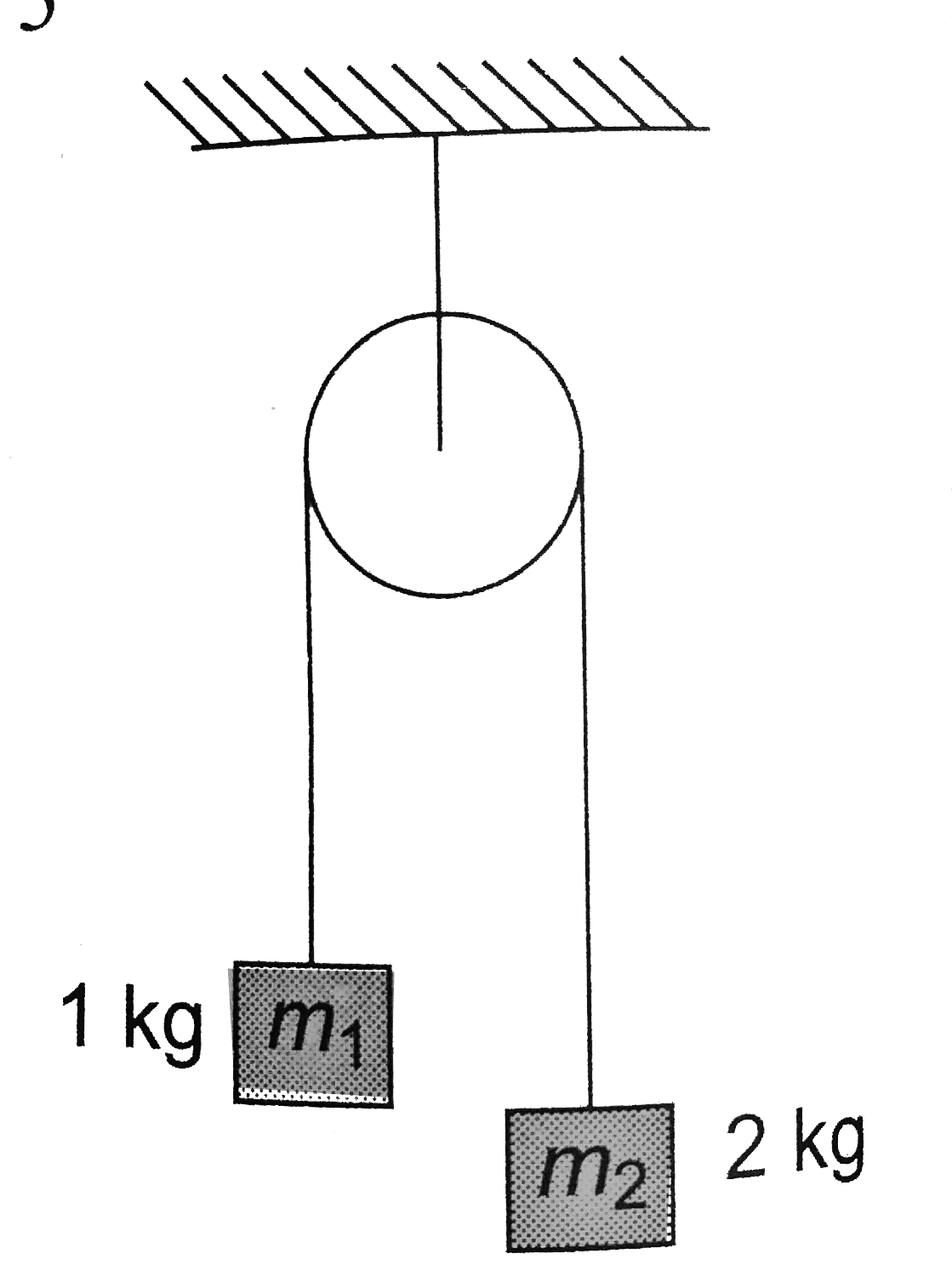 .
.
209m
409m
23m
13m
The correct Answer is:A
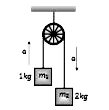
Here, m1=1kg,m2=2kg
The acceleration of the system is a=(m2−m1)gm1+m2=(2−1)g1+2=g3=103
Acceleration of the centre of mass is acm=m1a1+m2a2m1+m2=1(−a)+2(a)1+2
=1(−g3)+2(g3)3=g9=109
The distance travelled by the centre of mass in two seconds is
S=12acmt2=12×109×(2)2=209m
Similar Questions
Two bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be
View SolutionTwo masses m1=1kgandm2=2kg are connected by a light inextensible string and suspended by means of a weightness pulley as shown in the figure. Assuming that both the masses start from rest, the distance travelled by the centre of mass in two seconds is (Takeg=10ms−2.
 .
.
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g= 10 m//s^2 ).
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms^(-2) )
View SolutionTwo masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane Θ. The gangle of inclination of the plane is 0. Take g=10ms−2.
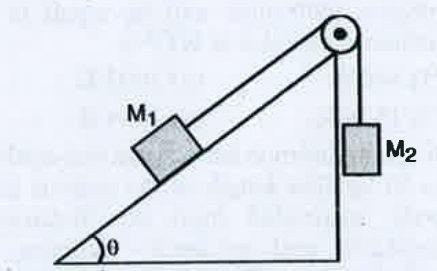
If M1=10kg. M2=5kg, Θ=30, the acceleration of mass M2 is
View SolutionIn the Atwood's machine shown in Fig. m_1 = 7 kg and m_2 = 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley of radius 5 cm. When the system is released from rest the heavier mass is found to fall 1 m in 2 s. Calculate the moment of inertia of the pulley ?
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g = 10 ms^(-2) , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is released from rest ,
View Solution
