The rate constant for a first order reaction is given by the following equation :
In k = 33.24 −2.0×104KT
The Activation energy for the reaction is given by ______ kJ mol−1 (In Nearest integer) (Given : R=8.3JK−1mol−1 )
To find the activation energy (Ea) for the given first-order reaction, we can start by comparing the provided equation with the Arrhenius equation. The Arrhenius equation is given by:
lnk=lnA−EaRT
Where:
- k is the rate constant,
- A is the pre-exponential factor (frequency factor),
- Ea is the activation energy,
- R is the universal gas constant,
- T is the temperature in Kelvin.
Given the equation:
lnk=33.24−2.0×104T
We can identify that:
−EaR=−2.0×104T
From this, we can deduce that:
EaR=2.0×104T
Now, we can rearrange this to find Ea:
Ea=2.0×104⋅R
Substituting the value of R:
R=8.314J K−1mol−1=8.314×10−3kJ K−1mol−1
Now, substituting R into the equation for Ea:
Ea=2.0×104⋅8.314×10−3
Calculating this gives:
Ea=2.0×104⋅8.314×10−3=166.28kJ mol−1
Finally, rounding to the nearest integer:
Ea≈166kJ mol−1
Thus, the activation energy for the reaction is:
166kJ mol−1
- k is the rate constant,
- A is the pre-exponential factor (frequency factor),
- Ea is the activation energy,
- R is the universal gas constant,
- T is the temperature in Kelvin.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION B)
1 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - CHEMISTRY (SECTION A)
19 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - CHEMISTRY (SECTION-B)
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Chemistry (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
The rate constant for the first order decomposition of H2O2 is given by the following equation : log K = 14.2 - 1.0×104TK
Calculate Ea for this reaction and rate constant k if its half life period be 200 minutes. (Given : R = 8.314 JK−1mol−1)
View SolutionThe rate constant for a first order decomposition reaction is given by log K=10 - 1000/T .Then,what will be activation energy in kcal/mol?
View Solution
Knowledge Check
The activation energy of a reaction is 58.3 kJ mol−1. The ratio of rate constants at 305 K and 300 K is about (R= 8.3 J K−1mol−1)
A1.25B1.5C1.75D2The rate constant of a first orrder reaction becomes six times when the temperature is raised from 350 K to 400 K. Calculate the activation energy of the reaction (R=8.314 JK−1 mol−1)
A4.17 kJ mol−1B41.7 kJ mol−1C417.0 kJ mol−1D417.0 kJ mol−1The rate constant for a first order reaction becomes six times when the temperature is raised from 350 K to 400 K. Calculate the activation energy for the reaction
[R=8.314JK−1mol−1]A4.17kJmol−1B41.7kJmol−1C417.0kJmol−1D4170kJmol−1
For the reaction A→B, the rate constant k (in s−1) is given by
log10k=20.35−(2.47×103)T
The energy of activation in kJ mol−1 is ________ . (Nearest integer)
[Given : R=8.314JK−1mol−1]
View SolutionThe rate constant for a first order decomposition reaction is given by "log K=10−1000T .Then,what will be activation energy in kcal/mol?
View SolutionThe rate constant (k) of a rection is measured different temperatures (T) , and the data are plotted in the given figure . The activation energy of the reaction in kJmol−1 is : (R is gas constant )
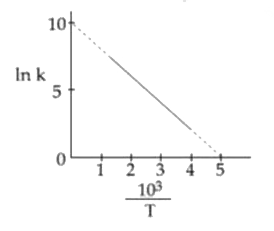
View SolutionIf the half-lives of the first order reaction at 350 K and 300 K are 2 and 20 seconds respectively, the activation energy of the reaction in kJ mol−1 is :
View SolutionIn the Arrhenius plot of ln k vs 1T , a linear plot is obtained with a slope of −2×104 K . The energy of activation of the reaction (in kJ mole−1) is (R value is 8.3 JK−1mol−1)
View Solution
