Assertion: If in a ΔABC, a line DE || BC, intersects AB in D and AC in E, then ABAD=ACAE.
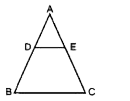
Reason: If a line is drawn parallel to one side of a triangle intersecting the other two sides, then the other two sides are divided in the same ratio.
Both the Assertion and the Reason are correct and the Reason is the correct explanation of the Assertion.
Both-the Assertion.and the Reason are.correct but the Reason is not the correct explanation of the Assertion.
Assertion is true but the Reason is false.
Assertion is false but the Reason is true.
The correct Answer is:A
Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Case Based Questions
12 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Passage Based Questions
7 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Very Short Answer Type Questions
12 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points. Prove that the other two sides are divided in the same ratio.
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionProve that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View SolutionIf in a ΔABC; a line DE||BC; intersects AB in D and AC in E; Then AB/ AD = AC/AE
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View Solution
