The straight line L≡x+y+1=0andL1≡x+2y+3=0 are intersecting. m is the slope of the straight line L2 such that L is the bisector of the angle between L1andL2 . The value of m2+1 is equal to
The correct Answer is:5
Similar Questions
Knowledge Check
In xy-plane, a straight line L1 bisects the 1st quadrant and another straight line L2 trisects the 2nd quadrant being closer to the axis of y . The acute angle between L1andL2 is
A60∘B120∘C90∘D75∘The lines L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q, respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R.
Statement 1 : The ratio PR : RQ equals 2√2:√5.
Statement 2: In any triangle, bisector of an angle divides the triangle into two similar triangles.1AStatement 1 is true, statement 2 is false.BStatement 1 is true, statement 2 is true, statement 2 is the correct explanation of statement1.CStatement 1 is true, statement 2 is true, statement 2 is not the correct explanation of statement 1.DStatement 1 is false, statement 2 is true.The lines L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively . The bisectors of the acute angle between L1 and L2 intersect L3 at R .
Statement 1 : The ratio PR : RQ equals 2√2:√5
Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .AStatement -1 is True , Statement - 2 is true , Statement- 2 is a correct explanation for statement - 14BStatement-1 is True , Statement-2 is True , Statement -2 is not a correct explanation for Statement - 1 .CStatement-1 is True , Statement - 2 is False .DStatement - 1 is False , Statement -2 is True .
The slope of the line that bisects the angle formed by the lines l1 and l2 if l1 has a slope of 2 and l2 is a vertical line can be
View SolutionThe lines L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively . The bisectors of the acute angle between L1 and L2 intersect L3 at R .
Statement 1 : The ratio PR : RQ equals 2√2:√5
Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
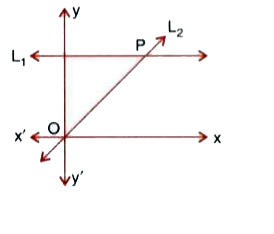
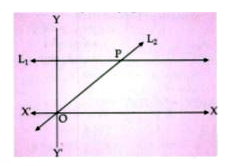
View SolutionIn the given figure, Given equation of line L1 is y = 4.
Write the slope of line L2 if L2 is the bisector of angle O.
View SolutionThe lines L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively . The bisectors of the acute angle between L1 and L2 intersect L3 at R .
Statement 1 : The ratio PR : RQ equals 2√2:√5
Statement - 2 : In any triangle , bisector of an angle divides the triangle into two similar triangles .
View SolutionLines L1:y−c=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R.
Statement I The ratio PR:RQ equals 2√2:√5.
Because
Statement II In any triangle, bisector of an angle divides the triangle into two similar triangles.
View Solution