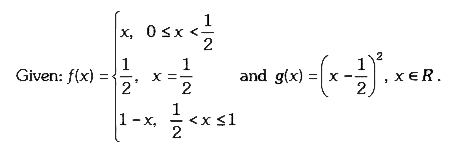
Then the area (in sq. units) of the region bounded by the curves, y =

Given : $f (x) ⎧ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎩ \begin{matrix} x, & 0 \leq x < \frac{1}{2} \frac{1}{2}, & x = \frac{1}{2} 1 - x, & \frac{1}{2} < x \leq 1 \end{matrix}$ and $g (x) = {(x - \frac{1}{2})}^{2}, x \in R$ . Then the area (in sq. units) of the region bounded by the curves, $y = f (x)$ and $y = g (x)$ between the lines, $2 x = 1$ and $2 x = \sqrt{3}$ , is :
A $\frac{\sqrt{3}}{4} - \frac{1}{3}$
B $\frac{1}{3} + \frac{\sqrt{3}}{4}$
C $\frac{1}{2} + \frac{\sqrt{3}}{4}$
D $\frac{1}{2} - \frac{\sqrt{3}}{4}$
The area (in sq units) of the region bounded by the curve $2 x = y^{2} - 1 and x = 0$ is
A $1 / 3$
B $2 / 3$
C1
D2
The area (in sq units) of the region bounded by the curves $y = e^{x}$ , $y = {log}_{e}$ x and lines x = 1, x = 2 is
A ${(e - 1)}^{2}$
B $e^{2} - e + 1$
C $e^{2} - e + 1 - 2 {log}_{e} 2$
D $e^{2} + e - 2 {log}_{e} 2$

Then the area (in sq. units) of the region bounded by the curves, $y = f (x) and y = g (x)$ between the lines, $2 x = 1 and 2 x = \sqrt{3}$ , is