Eight number 3,5,7,2k,12,15,21,27 are in increasing order and if mean deviation about median is 6. Then median of data is
To solve the problem step by step, we will first identify the median of the given numbers and then use the information about the mean deviation to find the value of k.
1. Identify the Numbers: The numbers given are 3,5,7,2k,12,15,21,27.
2. Order of the Numbers: Since the numbers are in increasing order, we need to ensure that 2k fits correctly within the sequence. Thus, we have the following inequalities:
- 2k≥7 (so k≥3.5)
- 2k≤12 (so k≤6)
Therefore, k must be in the range 3.5≤k≤6.
3. Finding the Median: Since there are 8 numbers, the median will be the average of the 4th and 5th numbers in the ordered list. Thus, the median M can be calculated as:
M=2k+122=k+6
4. Mean Deviation about the Median: The mean deviation about the median is given as 6. The mean deviation is calculated as follows:
Mean Deviation=1n∑|xi−M|
where n is the number of elements and xi are the elements of the dataset.
5. Calculating Deviations: We need to calculate the absolute deviations from the median M=k+6:
- For 3: |3−(k+6)|=|k+3|
- For 5: |5−(k+6)|=|k+1|
- For 7: |7−(k+6)|=|k−1|
- For 2k: |2k−(k+6)|=|k−6|
- For 12: |12−(k+6)|=|6−k|
- For 15: |15−(k+6)|=|9−k|
- For 21: |21−(k+6)|=|15−k|
- For 27: |27−(k+6)|=|21−k|
6. Summing the Deviations: We will sum these absolute deviations:
Sum of Deviations=|k+3|+|k+1|+|k−1|+|k−6|+|6−k|+|9−k|+|15−k|+|21−k|
7. Setting Up the Equation: The mean deviation is given as 6, so we set up the equation:
|k+3|+|k+1|+|k−1|+|k−6|+|6−k|+|9−k|+|15−k|+|21−k|8=6
This implies:
|k+3|+|k+1|+|k−1|+|k−6|+|6−k|+|9−k|+|15−k|+|21−k|=48
8. Solving for k: After calculating the sum of the deviations and simplifying, we find:
6k−42=48
6k=90⟹k=15
9. Finding the Median: Now substituting k back to find the median:
M=k+6=15+6=21
Final Answer:
The median of the data is 21.
- 2k≥7 (so k≥3.5)
- 2k≤12 (so k≤6)
M=2k+122=k+6
Mean Deviation=1n∑|xi−M|
where n is the number of elements and xi are the elements of the dataset.
- For 3: |3−(k+6)|=|k+3|
- For 5: |5−(k+6)|=|k+1|
- For 7: |7−(k+6)|=|k−1|
- For 2k: |2k−(k+6)|=|k−6|
- For 12: |12−(k+6)|=|6−k|
- For 15: |15−(k+6)|=|9−k|
- For 21: |21−(k+6)|=|15−k|
- For 27: |27−(k+6)|=|21−k|
Sum of Deviations=|k+3|+|k+1|+|k−1|+|k−6|+|6−k|+|9−k|+|15−k|+|21−k|
|k+3|+|k+1|+|k−1|+|k−6|+|6−k|+|9−k|+|15−k|+|21−k|8=6
This implies:
|k+3|+|k+1|+|k−1|+|k−6|+|6−k|+|9−k|+|15−k|+|21−k|=48
6k−42=48
6k=90⟹k=15
M=k+6=15+6=21
The median of the data is 21.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the mean deviation about median for the following data.
 A10.34B10.50C10.40D10.37
A10.34B10.50C10.40D10.37mean deviation about median for the following data 2,5,7,2,4,6,10,12,5
A2.4B3C1.9DNone of these
Find the mean deviation about the median for the data in Question
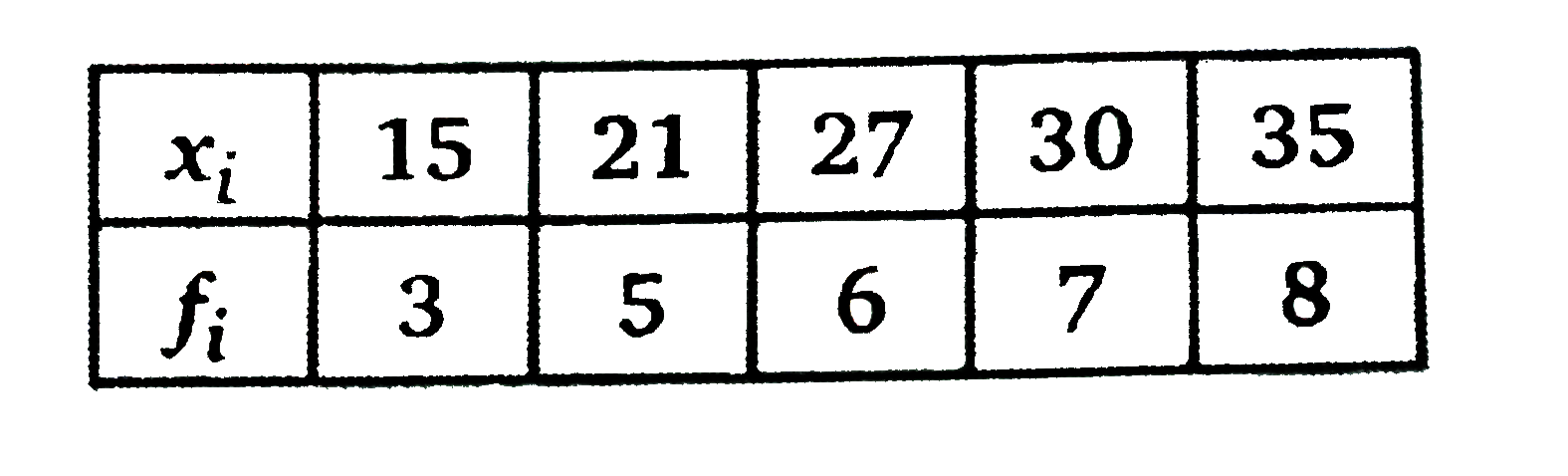
View SolutionFind the mean deviation about the median for the following data:
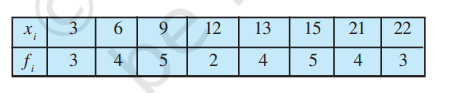
View SolutionCalculate the mean deviation about median for the following data:

View SolutionCalculate the mean deviation about median for the following data :
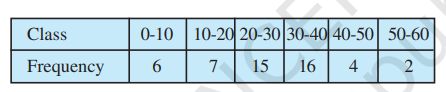
View SolutionCalculate the mean deviation about median for the following data:

View SolutionCalculate the mean deviation about median for the following data :
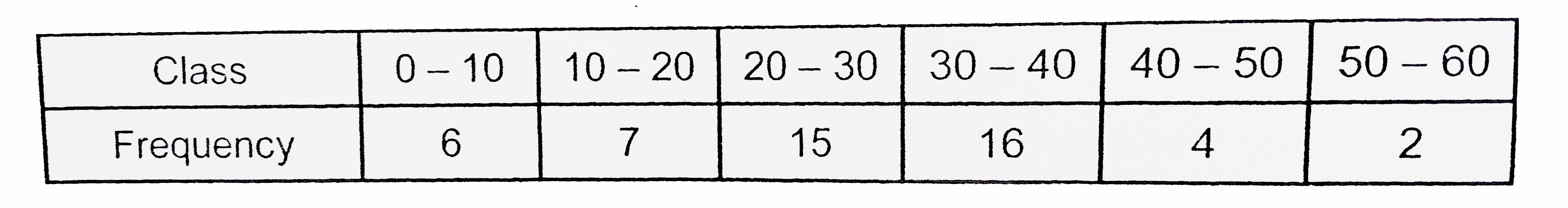
View Solution


