For 7 mole of monoatomic ideal gas calculate ΔU. If ΔT=40K
3492 J
5820 J
8148 J
2328 J
To calculate the change in internal energy (ΔU) for 7 moles of a monoatomic ideal gas with a temperature change (ΔT) of 40 K, we can use the formula for the change in internal energy of an ideal gas:
ΔU=32nRΔT
Where:
- n = number of moles of the gas
- R = universal gas constant (approximately 8.314 J/(mol·K))
- ΔT = change in temperature in Kelvin
1. Identify the values:
- Number of moles, n=7 moles
- Change in temperature, ΔT=40 K
- Universal gas constant, R=8.314 J/(mol·K)
2. Substitute the values into the formula:
ΔU=32×7×8.314×40
3. Calculate the multiplication:
- First, calculate 32×7=10.5
- Then, calculate 10.5×8.314=87.305
- Finally, calculate 87.305×40=3492.2
4. Round off the result:
- Rounding 3492.2 gives 3492 J.
Final Answer:
ΔU≈3492 J
- n = number of moles of the gas
- R = universal gas constant (approximately 8.314 J/(mol·K))
- ΔT = change in temperature in Kelvin
- Number of moles, n=7 moles
- Change in temperature, ΔT=40 K
- Universal gas constant, R=8.314 J/(mol·K)
ΔU=32×7×8.314×40
- First, calculate 32×7=10.5
- Then, calculate 10.5×8.314=87.305
- Finally, calculate 87.305×40=3492.2
- Rounding 3492.2 gives 3492 J.
ΔU≈3492 J
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Enthalpy of 1 mole monoatomic ideal gas is equals to :-
A32RTB52RTCRTD2 RT - Question 2 - Select One
One mole of monoatomic ideal gas at T(K) is exapanded from 1L to 2L adiabatically under constant external pressure of 1 atm . The final tempreture of gas in kelvin is
ATBT25/3−1CT−23×0.0821DT+23×0.0821 - Question 3 - Select One or More
For one mole of an ideal gas (δPδT)V(δVδT)P(δVδP)T=
A−1BR2P2CR2P2D+1
The heat required to increase the temperature of 4 moles of a monoatomic ideal gas from 273 K to 473 K at constant volume is
View SolutionOne mole of carbon undergoes incomplete combustion to produce carbon monoxide, Calculate (ΔH−ΔU) for the formation of CO at 298 K. Given R = 8.314 JK−1mol−1.
View SolutionThe entropy of v=4.0 moles of an ideal gas increases by ΔS=23J/K due to the isothermal expansion. How many times should the volume v=4.0 moles of the gas be increased ?
View SolutionIn a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by TΔX, where T is temperature of the system and ΔT is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas x=32R h(TTA)+Rh)(VVA). Here, R is gas constant, V is volume of gas, TAand TA are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.
If the process on one mole of monatomic ideal gas is as shown in the TV-diagram with P0V0=13RT0, the correct match is,

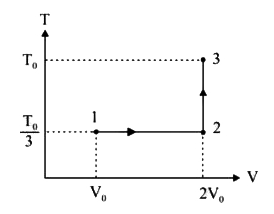 View Solution
View SolutionOne mole of a monoatomic ideal gas is mixed with one mole of a diatomic ideal gas . The molar specific heat of the mixture at constant volume is
View Solution


