For a binomial probability distribution , sum and product of mean and variance are 24 and 128 respectively . If P(x>n−3)=k2n then value of K is
To solve the problem, we need to analyze the given information about the binomial probability distribution. We know that the sum and product of the mean and variance are given as 24 and 128, respectively. Let's denote:
- Mean (μ) = np
- Variance (σ²) = npq = np(1-p)
Step 1: Set up the equations
From the problem, we have:
1. μ+σ2=24
np+np(1−p)=24
Simplifying, we get:
np(1+(1−p))=24⟹np(2−p)=24(1)
2. μ⋅σ2=128
np⋅np(1−p)=128⟹n2p2(1−p)=128(2)
Step 2: Solve the equations
From equation (1):
np(2−p)=24⟹np=242−p(3)
Substituting equation (3) into equation (2):
(242−p)2p2(1−p)=128
Step 3: Simplify the equation
Expanding this gives:
576p2(1−p)(2−p)2=128
Cross-multiplying:
576p2(1−p)=128(2−p)2
Expanding the right side:
576p2(1−p)=128(4−4p+p2)
576p2−576p3=512−512p+128p2
Rearranging gives:
448p2−576p3+512p−512=0
Dividing through by 16:
28p2−36p3+32p−32=0
Step 4: Factor the cubic equation
This cubic equation can be solved using numerical methods or by finding rational roots. Testing p=12:
28(12)2−36(12)3+32(12)−32=0
This gives:
28⋅14−36⋅18+16−32=0
Calculating:
7−4.5+16−32=0
This confirms p=12.
Step 5: Find n
Substituting p=12 back into equation (3):
np=242−12=2432=16⟹n=32
Step 6: Calculate P(X>n−3)
Now, we need to find P(X>n−3)=P(X>29):
P(X>29)=P(X=30)+P(X=31)+P(X=32)
Using the binomial probability formula:
P(X=k)=(nk)pkqn−k
where q=1−p=12.
Calculating:
P(X=30)=(3230)(12)30(12)2=(3230)(12)32
P(X=31)=(3231)(12)31(12)1=(3231)(12)32
P(X=32)=(3232)(12)32=(3232)(12)32
Thus,
P(X>29)=((3230)+(3231)+(3232))(12)32
Calculating the binomial coefficients:
(3230)=(322)=32×312=496
(3231)=32
(3232)=1
So,
P(X>29)=(496+32+1)(12)32=529(12)32
Final Result
Thus, k=529.
- Variance (σ²) = npq = np(1-p)
From the problem, we have:
1. μ+σ2=24
np+np(1−p)=24
Simplifying, we get:
np(1+(1−p))=24⟹np(2−p)=24(1)
np⋅np(1−p)=128⟹n2p2(1−p)=128(2)
From equation (1):
np(2−p)=24⟹np=242−p(3)
(242−p)2p2(1−p)=128
Expanding this gives:
576p2(1−p)(2−p)2=128
Cross-multiplying:
576p2(1−p)=128(2−p)2
Expanding the right side:
576p2(1−p)=128(4−4p+p2)
576p2−576p3=512−512p+128p2
Rearranging gives:
448p2−576p3+512p−512=0
Dividing through by 16:
28p2−36p3+32p−32=0
This cubic equation can be solved using numerical methods or by finding rational roots. Testing p=12:
28(12)2−36(12)3+32(12)−32=0
This gives:
28⋅14−36⋅18+16−32=0
Calculating:
7−4.5+16−32=0
This confirms p=12.
Substituting p=12 back into equation (3):
np=242−12=2432=16⟹n=32
Now, we need to find P(X>n−3)=P(X>29):
P(X>29)=P(X=30)+P(X=31)+P(X=32)
Using the binomial probability formula:
P(X=k)=(nk)pkqn−k
where q=1−p=12.
P(X=30)=(3230)(12)30(12)2=(3230)(12)32
P(X=31)=(3231)(12)31(12)1=(3231)(12)32
P(X=32)=(3232)(12)32=(3232)(12)32
P(X>29)=((3230)+(3231)+(3232))(12)32
Calculating the binomial coefficients:
(3230)=(322)=32×312=496
(3231)=32
(3232)=1
So,
P(X>29)=(496+32+1)(12)32=529(12)32
Thus, k=529.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In binomial probability distribution, mean is 3 and standard deviation is 32. Then the value of p is
A14B34C12D13 - Question 2 - Select One
Mean and variance of a binomial variate X are 4 and 2 respectively Then P(X=1)=……
A132B116C18D14 - Question 3 - Select One
In a binomial distribution the mean is 15 and variance is 10. Then, parameter n is
A28B16C45D25
In a binomial distribution, sum and product of mean and variance of a binomial distribution is 5and 6 respectively, find the distribution.
View SolutionIf the mean and variance of a binomial variable X are 2 and 1 respectively. Find P(X≥1) .
View SolutionThe probability distribution of X is as follows:
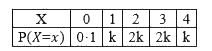
Find k and P [X<2].View SolutionMean and Variance of a binomial variance are 4 and 4/3 respectively then P(X≥1) will be
View SolutionIn a binomial distribution, the mean is 4 and the variance is 3. What is the mode?
View Solution

