Two dice are thrown at the same time. What is the probability that the sum of the two numbers appearing on the top of the dice is
(i) 8 ?
(ii) 13 ?
(iii) less than or equal to 12?
To solve the problem, we will calculate the probabilities for each part step by step.
Total Outcomes
When two dice are thrown, each die has 6 faces. Therefore, the total number of outcomes when two dice are thrown is:
6×6=36
(i) Probability that the sum is 8
1. Find the favorable outcomes for the sum of 8:
- The pairs that give a sum of 8 are:
- (2, 6)
- (3, 5)
- (4, 4)
- (5, 3)
- (6, 2)
- Total favorable outcomes = 5
2. Calculate the probability:
P(sum=8)=Number of favorable outcomesTotal outcomes=536
(ii) Probability that the sum is 13
1. Find the favorable outcomes for the sum of 13:
- The maximum sum with two dice is 12 (6 + 6). Therefore, there are no outcomes where the sum is 13.
- Total favorable outcomes = 0
2. Calculate the probability:
P(sum=13)=036=0
(iii) Probability that the sum is less than or equal to 12
1. Find the favorable outcomes for the sum less than or equal to 12:
- Since the maximum sum with two dice is 12, all outcomes (36) are favorable.
- Total favorable outcomes = 36
2. Calculate the probability:
P(sum≤12)=3636=1
Summary of Results
- (i) Probability that the sum is 8: 536
- (ii) Probability that the sum is 13: 0
- (iii) Probability that the sum is less than or equal to 12: 1
When two dice are thrown, each die has 6 faces. Therefore, the total number of outcomes when two dice are thrown is:
6×6=36
1. Find the favorable outcomes for the sum of 8:
- The pairs that give a sum of 8 are:
- (2, 6)
- (3, 5)
- (4, 4)
- (5, 3)
- (6, 2)
- Total favorable outcomes = 5
P(sum=8)=Number of favorable outcomesTotal outcomes=536
1. Find the favorable outcomes for the sum of 13:
- The maximum sum with two dice is 12 (6 + 6). Therefore, there are no outcomes where the sum is 13.
- Total favorable outcomes = 0
P(sum=13)=036=0
1. Find the favorable outcomes for the sum less than or equal to 12:
- Since the maximum sum with two dice is 12, all outcomes (36) are favorable.
- Total favorable outcomes = 36
P(sum≤12)=3636=1
- (i) Probability that the sum is 8: 536
- (ii) Probability that the sum is 13: 0
- (iii) Probability that the sum is less than or equal to 12: 1
Topper's Solved these Questions
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - Section D6videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - Section E12videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - Section B7videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION C10videos
SAMPLE PAPER 2022 TERM II
Similar Questions
Two dice, one blue and one grey, are thrown at the same time. Write down all the possible outcomes. What is the probability that the sum of the two numbers appearing on the top of the dice is
(i)8 ,
(ii) 13?
(ii) less than or equal to 12?View Solution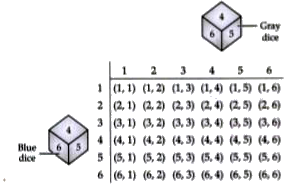
Two dice, one blue and one grey are thrown at the same time.
What is the probability that the sum of the two numbers appearing on the top of the dice is 8 ?View Solution
Knowledge Check
- Question 1 - Select One
Two dices are thrown simultaneously. What is the probability that the sum of the numbers appearing on them is a prime number?
A5/12B1/2C7/12D2/3
Two dice are thrown at the same time. Find the probability of getting the sum of the dice is 8.
View Solution
Two dice, one blue and one grey are thrown at the same time.
Find the Probability that the sum of the two numbers appearing on the top to the dice is 11.View SolutionA black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability? that the sum of the numbers appearing on the top of the dice is less than or equal to 12? that the product of numbers appearing on the top of the dice is less than 9. (iii) that the difference of the numbers appearing on the top of the two dice is 2.
View SolutionTwo different dice are thrown simultaneously. What is the probability that the sum of two number appearing on the top of dice is.
(i) 9 (ii) 10 (iii) at least 10 (iv) 13 (v) less than or equal 12
(vi) a multiple of 2 on one die and a multiple of 3 on the other die ?View SolutionTwo dice are thrown simultaneously. What is the probability that the sum of the number appearing on the dice is
(i) 7? (ii) a prime number? (iii) 1?View SolutionTwo dice are thrown. What is the probability that the sum of the numbers appearing on the two dice is 11, it 5 appears on the first?
View SolutionTwo dice are thrown at the same time. Determine the probability that the difference of the numbers on the two dice is :
(i) 0. (ii) 2.View Solution

