ABCD is a trapezium with AD ∥ BC and AD = 4cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB =1/2, then BC =
6 cm
7 cm
8 cm
9 cm
To solve the problem, we will follow these steps:
1. Draw the trapezium ABCD:
We have a trapezium ABCD where AD is parallel to BC and AD = 4 cm.
2. Identify the point of intersection of the diagonals:
The diagonals AC and BD intersect at point O. We are given that AO/OC = DO/OB = 1/2.
3. Set up the ratios:
Since AO/OC = 1/2, we can denote AO as x and OC as 2x. Similarly, since DO/OB = 1/2, we can denote DO as y and OB as 2y.
4. Use the property of similar triangles:
Triangles AOD and BOC are similar because AD is parallel to BC. By the AA (Angle-Angle) similarity criterion, we can establish the following ratio:
AOOC=ADBC
5. Substituting the known values:
We know AO = x, OC = 2x, and AD = 4 cm. Therefore, we can write:
x2x=4BC
Simplifying the left side gives:
12=4BC
6. Cross-multiply to solve for BC:
Cross-multiplying gives:
1⋅BC=2⋅4
Thus:
BC=8 cm
7. Conclusion:
The length of BC is 8 cm.
We have a trapezium ABCD where AD is parallel to BC and AD = 4 cm.
The diagonals AC and BD intersect at point O. We are given that AO/OC = DO/OB = 1/2.
Since AO/OC = 1/2, we can denote AO as x and OC as 2x. Similarly, since DO/OB = 1/2, we can denote DO as y and OB as 2y.
Triangles AOD and BOC are similar because AD is parallel to BC. By the AA (Angle-Angle) similarity criterion, we can establish the following ratio:
AOOC=ADBC
We know AO = x, OC = 2x, and AD = 4 cm. Therefore, we can write:
x2x=4BC
Simplifying the left side gives:
12=4BC
Cross-multiplying gives:
1⋅BC=2⋅4
Thus:
BC=8 cm
The length of BC is 8 cm.
Topper's Solved these Questions
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - SECTION-B7videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - SECTION-C8videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - Section E12videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION C10videos
SAMPLE PAPER 2022 TERM II
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a regular trapezium in which AD∣∣BC Diagonal AC and BD intersect at O, AO = 3 CO = X - 3 BO = 3X - 19 , DO = X - 5 . Find X
A−8,9B8,−9C−8,−9D8,9 - Question 2 - Select One
In a trapezium ABCD, the diagonals AC and BD interserted other at O such that OB:OD=3:1 then the ratio of area of ΔAOB:ΔCOD is :
A3:1B1:4C9:1Dcan't be determined - Question 3 - Select One
In a trapezium ABCD, the diagonals AC and BD interserted other at O such that OB:OD=3:1 then the ratio of area of ΔAOB:ΔCOD is :
A3:1B1:4C9:1Dcan't be determined
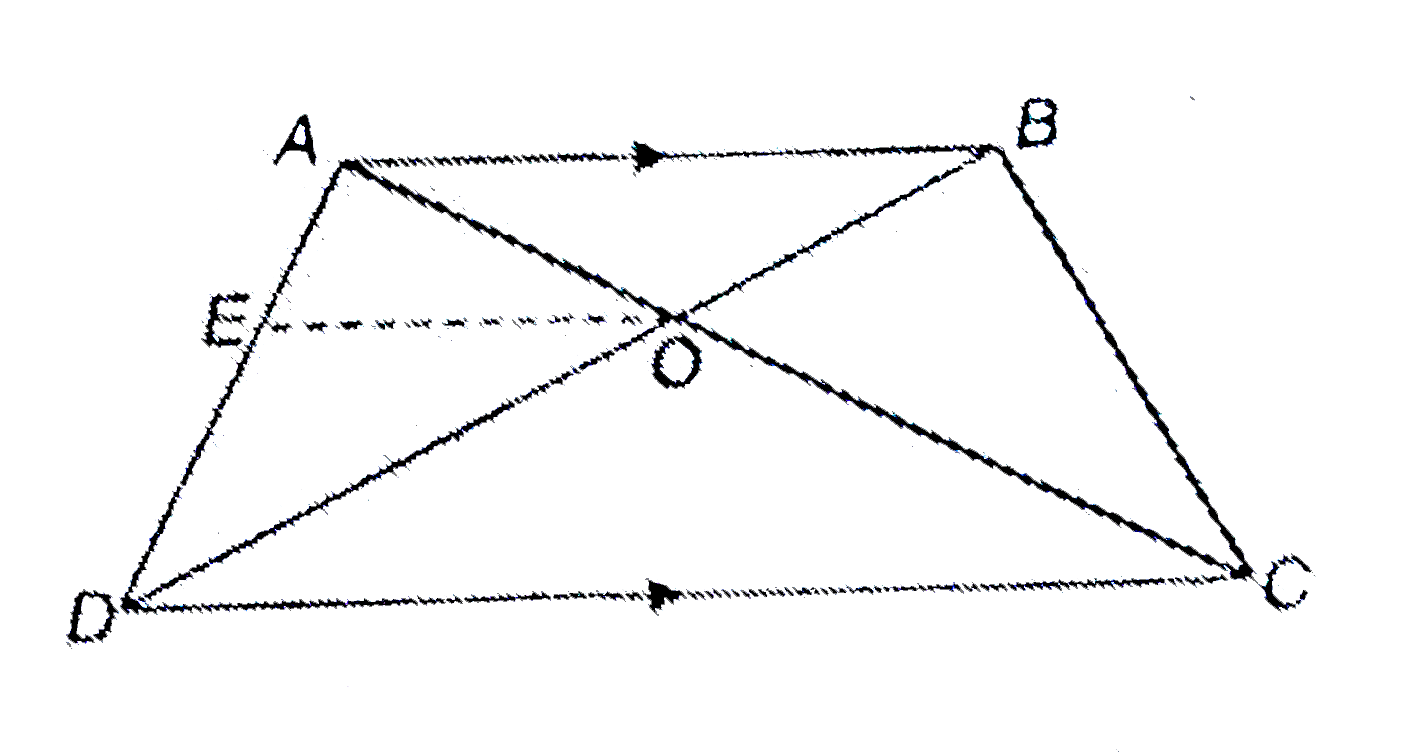
ABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View Solutionif ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionLength of parallel sides AB and CD of a trapezium are respectively 10 cm and 14 cm. If its diagonals AC and BD intersects at O then AO : OC is
View SolutionABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
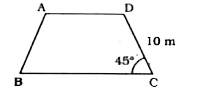 View Solution
View Solution