Prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.
Using the above theorem prove that a line through the point of intersection of the diagonals and parallel to the base of the trapezium divides the non parallel sides in the same ratio.
To prove that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio, we can follow these steps:
1. Draw the Triangle:
Let triangle ABC be given, where we draw a line DE parallel to side AB that intersects sides AC and BC at points D and E, respectively.
2. Label the Points:
We label the points as follows: A, B, C for the vertices of the triangle, and D and E for the points where the line intersects the sides AC and BC.
3. Apply Basic Proportionality Theorem:
According to the Basic Proportionality Theorem (also known as Thales' theorem), if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Therefore, we can write:
ADDC=AEEB
This means that the segments on sides AC and BC are in the same ratio.
4. Conclusion:
Thus, we have proved that if a line is drawn parallel to one side of a triangle, it divides the other two sides in the same ratio.
Using the Theorem for a Trapezium:
1. Draw the Trapezium:
Let trapezium ABCD be given, where sides AB and CD are parallel.
2. Draw the Diagonals:
Draw diagonals AC and BD, which intersect at point O.
3. Draw a Line Parallel to the Base:
Draw a line EF through point O parallel to the bases AB and CD, intersecting sides AD and BC at points E and F, respectively.
4. Apply the Theorem:
By the theorem we just proved, since EF is parallel to AB (and CD), we can apply the Basic Proportionality Theorem again:
AEED=AFFB
This shows that the non-parallel sides AD and BC are divided in the same ratio by the line EF.
5. Conclusion:
Hence, it is proved that a line through the point of intersection of the diagonals and parallel to the base of a trapezium divides the non-parallel sides in the same ratio.
Let triangle ABC be given, where we draw a line DE parallel to side AB that intersects sides AC and BC at points D and E, respectively.
We label the points as follows: A, B, C for the vertices of the triangle, and D and E for the points where the line intersects the sides AC and BC.
According to the Basic Proportionality Theorem (also known as Thales' theorem), if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Therefore, we can write:
ADDC=AEEB
This means that the segments on sides AC and BC are in the same ratio.
Thus, we have proved that if a line is drawn parallel to one side of a triangle, it divides the other two sides in the same ratio.
Let trapezium ABCD be given, where sides AB and CD are parallel.
Draw diagonals AC and BD, which intersect at point O.
Draw a line EF through point O parallel to the bases AB and CD, intersecting sides AD and BC at points E and F, respectively.
By the theorem we just proved, since EF is parallel to AB (and CD), we can apply the Basic Proportionality Theorem again:
AEED=AFFB
This shows that the non-parallel sides AD and BC are divided in the same ratio by the line EF.
Hence, it is proved that a line through the point of intersection of the diagonals and parallel to the base of a trapezium divides the non-parallel sides in the same ratio.
Topper's Solved these Questions
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - SECTION-E7videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2023 TERM IEXERCISE - SECTION-C8videos
SAMPLE PAPER 2023 TERM I
- BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE PAPER 2022 TERM IIEXERCISE - SECTION C10videos
SAMPLE PAPER 2022 TERM II
Similar Questions
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
View Solution
Knowledge Check
- Question 1 - Select One
If the line DE is drawn parallel | to the base BC of a triangle ABC by Intersecting the other two sides, then which of the following is the CORRECT equation for this case.
AABDB=ACECBADAB=DBECCADDB=ECAEDADDB=AEEC
If a line is drawn to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
View SolutionIf a line is drawn parallel to one side of a triangle to intersect the other two sides in disinct points, the other two sides are divided in the same ratio. Using this theoure. Find EC in if DE∣∣BC.
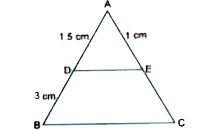 View Solution
View SolutionProve that , "If a line parallel to a side of a triangle intersects the remaining sides in two distinct points then the line divides the sides in the same proportion".
View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
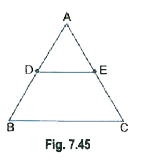 View Solution
View SolutionAny line parallel to the parallel sides of a trapezium divides the non-parallel sides proportionally.
View SolutionBasic proportionality Theorem or Thales Theorem - If a line is drawn parallel to one side of a triangle intersecting the other two sides; then it divides the two sides in the same ratio.
View SolutionIf a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, prove that the quadrilateral, so formed is cyclic.
View Solution

