The marks obtained by a set of students in an exam are recorded in a grouped frequency table. The maximum number of students are found to be in the range of (70-80) marks.
If the number of students in the ranges before and after the (70-80) range are equal, which of the following is the mode of the data?
70 marks
75 marks
80 marks
(mode cannot be found as frequency is not given)
To solve the problem, we need to find the mode of the data given the conditions stated in the question. Here’s the step-by-step solution:
Step 1: Identify the modal class
The question states that the maximum number of students is found in the range of 70-80 marks. Therefore, the modal class is 70-80.
Hint: The modal class is the class with the highest frequency.
Step 2: Define the variables
Let:
- f1 = frequency of the modal class (70-80)
- f0 = frequency of the class before the modal class (60-70)
- f2 = frequency of the class after the modal class (80-90)
According to the problem, the number of students in the ranges before and after the (70-80) range are equal. Thus, we can say:
- f0=f2
Let’s denote f0=f2=y and f1=x.
Hint: Assign variables to the frequencies for easier calculations.
Step 3: Use the mode formula
The formula for calculating the mode is given by:
Mode=L+f1−f02f1−f0−f2×h
Where:
- L = lower limit of the modal class = 70
- h = class width = 80 - 70 = 10
Substituting the values into the formula:
Mode=70+x−y2x−y−y×10
This simplifies to:
Mode=70+x−y2x−2y×10
Hint: Substitute the known values into the formula to simplify.
Step 4: Simplify the expression
Since f0=f2=y, we can rewrite the expression:
Mode=70+x−y2(x−y)×10
This further simplifies to:
Mode=70+102=70+5=75
Hint: Carefully simplify the fractions and perform the arithmetic operations.
Step 5: Conclusion
Thus, the mode of the data is:
Mode=75
Final Answer: The mode of the data is 75 marks.
The question states that the maximum number of students is found in the range of 70-80 marks. Therefore, the modal class is 70-80.
Let:
- f1 = frequency of the modal class (70-80)
- f0 = frequency of the class before the modal class (60-70)
- f2 = frequency of the class after the modal class (80-90)
- f0=f2
The formula for calculating the mode is given by:
- L = lower limit of the modal class = 70
- h = class width = 80 - 70 = 10
Since f0=f2=y, we can rewrite the expression:
Thus, the mode of the data is:
Topper's Solved these Questions
Similar Questions
The mean marks obtained by 300 students in a subject are 60. The mean of top 100 students was found to be 80 and the mean of last 100 students was found to be 50. The mean marks of the remaining 100 students are
View SolutionPercentage of marks of 35 students is given in the following grouped frequency distribution table.

How many students scored 70% and more than 70% of marks?
View Solution
Knowledge Check
The class, in which the marks of maximum number of students lies, is
 A40.5 to 50.5B50.5 to 60.5C60.5 to 70.5D70.5 to 80.5
A40.5 to 50.5B50.5 to 60.5C60.5 to 70.5D70.5 to 80.5The average marks obtained by 180 students in an examination is 50. If the average marks of passed students is 80 and that of the failed students is 40, then what is the number of students who failed the examination ?
A90B135C100D45The marks of 3 students A, B and C are in the ratio 10:12:15. If the maximum marks of the paper are 100, then the marks o fB cannot be in the range of
A20-30B40-50C70-80D80-90
Percentage of marks of 35 students is given in the following grouped frequency distribution table.

How many students scored less than 90% of marks?
View SolutionThe marks obtained (out of 100) by a class of 80 students are given below:

Construct a histogram to represent the data above
View SolutionMarks obtained by 100 students of a class are given below. Find out range and coefficient of range of the marks.
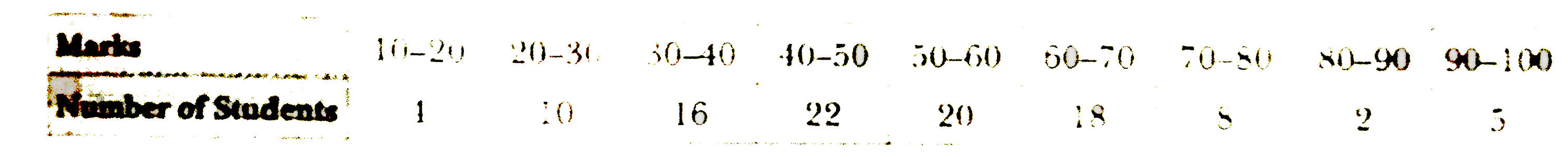
View SolutionStudy the given histogram that shows the marks obtained by students in an examination and answer the question that follows .
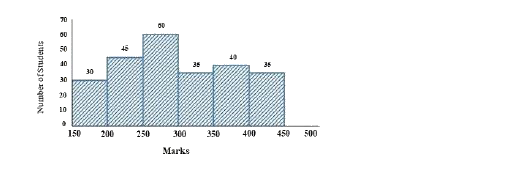
The number of students who obtained less than 250 marks is :
View SolutionStudy the given histogram that shows the marks obtained by students in examination and answer the question that follows

The number of students who obtained less than 200 marks is :
View Solution
