The constraints of a linear programming problem along with their graphs is shown below:
$x + 2 y \geq 3$
$x \geq 10$
$y \geq 0$

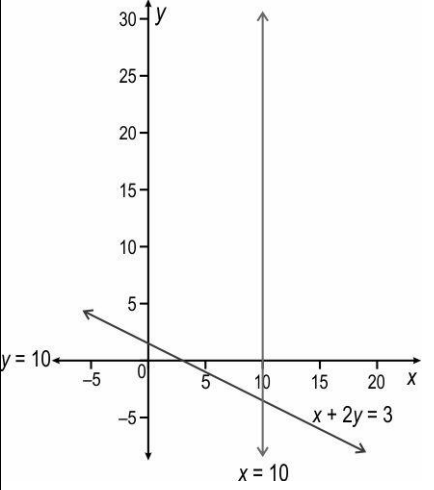
Which of the following objective functions has an optimal solution with respect to the above set of constraints?

Minimise $Z = x + y$

Minimise $Z = 0.5 x + y$

Maximise $Z = x + y$

Maximise $Z = 2 x + y$

Video Solution

Answer

Step by step video & image solution for The constraints of a linear programming problem along with their graphs is shown below: x + 2y ge 3 x ge 10 y ge 0 Which of the following objective functions has an optimal solution with respect to the above set of constraints? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS Additional Practice Questions

Topper's Solved these Questions

BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS
9videos
QUESTION BANK 2021

Knowledge Check

Question 1 - Select One
The linear programming problem minimiseZ=3x+2y subject to the constraints
$x + y \geq 8$
$3 x + 5 y \leq 15$
$x \geq 0, y \geq 0$ has
Aone solution
Bno feasible solution
Ctwo solutions
Dinfinitely many solution
Question 2 - Select One
In a linear programming problem, the constraints on the decision variables x and y are $x - 3 y \geq 0, y \geq 0, 0 \leq x \leq 3$ . The feasible region:
Ais not in the first quadrant
Bis bounded in the first quadrant
Cis unbounded in the first quadrant
Ddoes not exist
Question 3 - Select One
The solution set of
$x - 2 y \geq 0, 2 x - y \leq - 2, x \geq 0, y \geq 0$ is
AEmpty
BBounded
CNeither empty nor bounded
DNone of these

CBSE MODEL PAPER-Additional Practice Questions-Question

Home
Ask Doubt
Profile

The constraints of a linear programming problem along with their graphs is shown below: x+2y≥3 x≥10 y≥0 Which of the following objective functions has an optimal solution with respect to the above set of constraints?

Topper's Solved these Questions

Similar Questions

Knowledge Check

The linear programming problem minimiseZ=3x+2y subject to the constraints x+y≥8 3x+5y≤15 x≥0,y≥0 has

In a linear programming problem, the constraints on the decision variables x and y are x−3y≥0,y≥0,0≤x≤3. The feasible region:

The solution set of x−2y≥0,2x−y≤−2,x≥0,y≥0 is

CBSE MODEL PAPER-Additional Practice Questions-Question

The constraints of a linear programming problem along with their graphs is shown below:
$x + 2 y \geq 3$
$x \geq 10$
$y \geq 0$

Which of the following objective functions has an optimal solution with respect to the above set of constraints?

The linear programming problem minimiseZ=3x+2y subject to the constraints
$x + y \geq 8$
$3 x + 5 y \leq 15$
$x \geq 0, y \geq 0$ has

In a linear programming problem, the constraints on the decision variables x and y are $x - 3 y \geq 0, y \geq 0, 0 \leq x \leq 3$ . The feasible region:

The solution set of
$x - 2 y \geq 0, 2 x - y \leq - 2, x \geq 0, y \geq 0$ is