Let A be the event that the absolute difference between two randomly choosen real numbers in the sample space [0,60] is less than or equal to a.If P(A)=1136,then a is equal to
To solve the problem, we need to find the value of a such that the probability P(A)=1136, where A is the event that the absolute difference between two randomly chosen real numbers x and y in the interval (0,60) is less than or equal to a.
1. Understanding the Event:
The event A can be expressed as:
|x−y|≤a
This can be rewritten as:
−a≤x−y≤a
This means that x can be between y−a and y+a.
2. Setting Up the Sample Space:
The sample space for choosing x and y is the square defined by the coordinates (0,0), (60,0), (60,60), and (0,60). The area of this square is:
Area of sample space=60×60=3600
3. Finding the Area of the Event:
The area where |x−y|≤a is a band around the line x=y with width 2a. The vertices of this band will be constrained by the square's boundaries.
The area of the region defined by |x−y|≤a can be calculated as follows:
- The total area of the square minus the areas of the two triangles that are outside the band.
The triangles are formed at the corners of the square:
- The base and height of each triangle are 60−a.
- The area of one triangle is:
Area of triangle=12×(60−a)×(60−a)=(60−a)22
- Since there are two such triangles, the total area of the triangles is:
Total area of triangles=2×(60−a)22=(60−a)2
Therefore, the area of the event A is:
Area of event A=3600−(60−a)2
4. Setting Up the Probability Equation:
The probability P(A) is given by:
P(A)=Area of event AArea of sample space=3600−(60−a)23600
Setting this equal to 1136:
3600−(60−a)23600=1136
5. Solving for a:
Cross-multiplying gives:
36(3600−(60−a)2)=11×3600
Simplifying, we have:
129600−36(60−a)2=39600
Rearranging gives:
36(60−a)2=129600−39600=90000
Dividing by 36:
(60−a)2=2500
Taking the square root:
60−a=50or60−a=−50
Thus:
a=10ora=110(not valid since a≤60)
6. Final Answer:
Therefore, the value of a is:
10
The event A can be expressed as:
|x−y|≤a
This can be rewritten as:
−a≤x−y≤a
This means that x can be between y−a and y+a.
The sample space for choosing x and y is the square defined by the coordinates (0,0), (60,0), (60,60), and (0,60). The area of this square is:
Area of sample space=60×60=3600
The area where |x−y|≤a is a band around the line x=y with width 2a. The vertices of this band will be constrained by the square's boundaries.
- The total area of the square minus the areas of the two triangles that are outside the band.
- The base and height of each triangle are 60−a.
- The area of one triangle is:
Area of triangle=12×(60−a)×(60−a)=(60−a)22
- Since there are two such triangles, the total area of the triangles is:
Total area of triangles=2×(60−a)22=(60−a)2
Area of event A=3600−(60−a)2
The probability P(A) is given by:
P(A)=Area of event AArea of sample space=3600−(60−a)23600
Setting this equal to 1136:
3600−(60−a)23600=1136
Cross-multiplying gives:
36(3600−(60−a)2)=11×3600
Simplifying, we have:
129600−36(60−a)2=39600
Rearranging gives:
36(60−a)2=129600−39600=90000
Dividing by 36:
(60−a)2=2500
Taking the square root:
60−a=50or60−a=−50
Thus:
a=10ora=110(not valid since a≤60)
Therefore, the value of a is:
10
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let [x] be the greatest integer less than or equal to x, for a real number x. Then the following sum
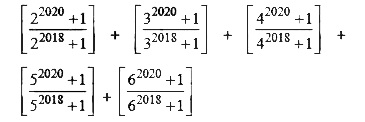
is-A80B85C90D95The difference between two numbers is 18. If four times the second number is less than three times the first number by 18, then what is the sum of these two numbers?
A100B80C86D92A die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P(A∪B) is (1) 35 (2) 0 (3) 1 (4) 25
A35B0C1D25
In how many ways, two different natural numbers can be selected, which less than or equal to 100 and differ by at most 10.
View SolutionLet a be a positive real number such that ∫a0ex−[x]dx=10e−9 where [x] is the greatest integer less than or equal to X. Then a equal to :
View SolutionLet A be 3×3 symmetric invertible matrix with real positive elements. Then the number of zero elements in A−1 are less than or equal to :
View SolutionLet A be 3×3 symmetric invertible matrix with real positive elements. Then the number of zero elements in A−1 are less than or equal to :
View SolutionLet [x] be the greatest integer less than or equal to x, for a real number x. Then the equation [x2]=x+1 has
View Solution
